Объясните как пользоваться тем, что находится в квадратных скобках.
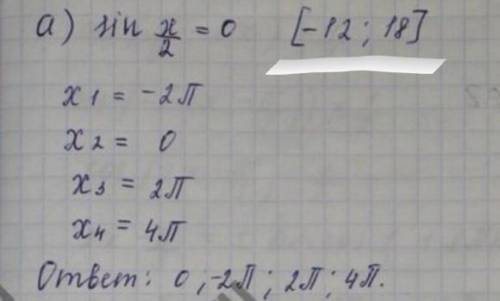
Другие вопросы по теме Математика
Популярные вопросы
- Кто из оперных певиц около 200 раз создал на сцене оброз айчурек...
3 - Дан треугольник АВС, периметр которого 42 см. на стороне АС...
3 - Скажите учёного сформулировавшего теорию о неравенстве...
2 - Найдите НОД чисел 180 и 253...
3 - Как думаете почему не у всех диалектных слов есть литературные...
2 - 4. Используя карту, совершите путешествие вокруг материка Северной...
3 - В топе по 1 день есть человек по именем dimashkulambekk и лайкнуть...
1 - Найдите нули функции и промежутки знакопостоянства ,...
2 - 5. Решите уравнение и выполните проверку:2(5х+15)+17=77...
3 - Составь стихотворение используя предложенную рифму (про героя...
2
Эти скобки показывают промежуток, из которого нужно выписать все корни, удовлетворяющие уравнение.
Так как это тригонометрическое уравнение, то не стоит забывать, чему равно значение числа пи.
В квадратных скобках - отрезок, на котором Вы должны перебрать свои ответы и записать те из них, которые в этот отрезок попадают. Вы решили уравнение, его видно, это sinx=0, откуда х/2=πк; к∈Z; х=2πк; к∈Z;
В отрезок попадают все углы от =-12радиаан до 18 радиан.
В одном радиане примерно 57°, значит, Вам задан отрезок от ≈-687.549° до ≈1031.32°.
Если Ваш ответ перевести в градусную меру, так привычнее? ТОГДА х=360°к; к-целое, выбираете такое, чтобы корень уравнения попал в указанный отрезок , если возьмем к=-2, то получим -720°, поэтому не подходит, если берем к=-1, получаем х=-360°, он подходит т.к. отрезок [-687.549°;1031.32°], дальше к=0, х=0°, опять сидит в отрезке, к=1, х=360°; подходит, к=2; х=720°; к=3; х=1080° не подходит. выходим за пределы отрезка. Теперь о радианах, умножаете например, на 2 получаете 4π=4*3.14≈12.56 радиан, еще остаетесь в отрезке, а уже при умножении на к=4 получаете 2π*4=8π≈24, но 24 больше 18.
И последнее. Вы бы могли не перебирать, а наверняка знать, какие к подойдут. для этого Вам надо было решить неравенство
-12≤2πк≤18; π≈3.14; -12≤6.28πк≤18, откуда -12/6.28≤(6.28/(6.28))к≤18к/6.28
-1.9≤к≤2.9; к -целые, поэтому в формулу корней 2πк надо подставлять к=-1, 0, 1, 2. Другие не подойдут.