Обчислити площу фігури, обмеженої заданими кривими: y=x, y=x+sinx, 0<=x<=П/6

Ответы

nazarzadorozhny 30.05.2023 22:00

Відповідь:

Покрокове пояснення:

На проміжку від 0 до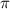 $\pi$ синус приймає додатні значення, а отже і на проміжку від 0 до 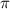$\pi$ \6. Тобто, пам'ятаючи про яку область визначення(область значень x, область значень аргумента) ми кажемо, можна стверджувати наступну нерівність sin(x) > 0. Пам'ятаючи, що x невід'ємний можемо отримати наступну нерівність x + sin(x) > x. Отже ці графіки на цій області визначення не перетинаються, а також ми знаємо, який графік знаходиться знизу, а який зверху.

Площа — це інтеграл. Область інтегрування дана. Площа графіку y=x очевидно менша за площу графіку y = x + sin(x), бо другий графік знаходиться над першим. Тобто знаходимо інтеграл, що відповідає більшій площ, і віднімаємо інтеграл, що відповідає меншій площі. Це буде плоша між цими графіками.

Але спам'ятаємо правило, що інтеграл суми дорівнює сумі інтегралів.

$\int\limits^{\pi / 6}_0 {x + sinx} \, dx = \int\limits^{\pi / 6}_0 {x} \, dx + \int\limits^{\pi / 6}_0 {sin(x)} \, dx$

$\int\limits^{\pi / 6}_0 {x + sin(x)} \, dx - \int\limits^{\pi / 6}_0 {x} \, dx =(\int\limits^{\pi / 6}_0 {sin(x)} \, dx + \int\limits^{\pi / 6}_0 {x} \, dx ) - \int\limits^{\pi / 6}_0 {x} \, dx = \int\limits^{\pi / 6}_0 {sin(x)} \, dx = -cos(x) |_0^{\pi / 6} = -cos(\pi/6) - (-cos(0)) = -\sqrt{3} /2 + 1 = 1 - \frac{\sqrt{3}}{2}$