1. Математика
  2. Обчислити площу фігури обмеженої

Обчислити площу фігури обмеженої лініями:​


Обчислити площу фігури обмеженої лініями:​

imuraveva imuraveva    1   13.05.2021 23:20    0

Ответы
Magistr126 Magistr126  13.05.2021 23:30

1) Найдём точки пересечения графиков:

y = 0.5x² ; y = 4-x

0.5x² = 4-x

x²+2x - 8 = 0

x = -4;

x = 2;

Построим графики двух функций (фото №1)

функция y = 4-x располагается выше y = 0.5x²,

по-этому площадь фигуры считается как :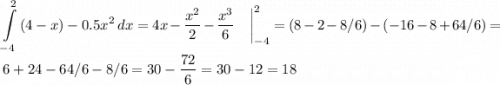\displaystyle \int\limits^{2}_{-4} {(4-x)-0.5x^2} \, dx = 4x -\frac{x^{2} }{2} -\frac{x^{3} }{6} \quad\bigg|^2_{-4} = (8 - 2 - 8/6)-(-16-8+64/6)=6+24-64/6-8/6 = 30-\frac{72}{6} =30-12=18

ответ: площадь равна 18 квадратных единиц


Обчислити площу фігури обмеженої лініями:​
Обчислити площу фігури обмеженої лініями:​
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Kattemrrr Kattemrrr  13.06.2019 18:10
:периметр прямоугольника, если площадь его равна 30 см2. длина 6 см. ширина неизвестно. 2) площадь прямоугольника, если его периметр равен 16 дм. длина 5 дм. ширина неизвестно....
Amelia2018 Amelia2018  13.06.2019 18:10
Две машины движутся на встречу друг другу со скоростями 60 км в ч и 80 км в ч. через какое время они встретятся, если расстояние между ними 140 км...
valwkebe valwkebe  13.06.2019 18:10
Туристы были в пути 2ч.третью часть этого времени они затратили на переправу через реку,30мин на привал,а остальное время-на пеший переход.сколько времени двигались туристы пешком?...
LEZENR LEZENR  13.06.2019 18:10
На производство одного изделия израсходовано: - материалов - 300 рублей - сырья, материалов - 6500 рублей - материалов - 300 рублей - комплектующих изделий - 100 рублей - заработная...
ольга240387 ольга240387  13.06.2019 18:10
Бабушка испекла 12 блинов. к ней пришли в гости внуки и стали есть блины. бабушка продолжила печь блины. пока бабушка пекла два блина внуки успевали съесть три. сколько блинов съели...
тигрц28 тигрц28  13.06.2019 18:10
Составьте уравнение и решите его: отцу и сыну вместе 54 года. через 3 года отец будет старше сына в 3 раза. сколько лет отцу? сколько лет сыну?...
kkkkkdashakkkk kkkkkdashakkkk  13.06.2019 18:10
Слова решето,решётка,прореха были когда-то родственными . найди старый корень в этих словах и укажи его значение....
Руфина157 Руфина157  13.06.2019 18:10
Решите неравенство 5(2х-7)-3 6-4(2-5х) изобразите на координатной прямой числовой промежуток, являющийся решением неравенства....
fiyyk fiyyk  13.06.2019 18:10
Нужен краткий конспект о жизни и творчестве и.с баха (в каких городах был, какие произведения написал, где работал? ) !...
никита20029 никита20029  13.06.2019 18:10
Решить укажи наименьшее общее кратное для чисел 5•7 и 2•7•11 заранее огромное...

Популярные вопросы