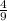Обчисліть кут між векторами:
a(-1;2;-2) і b(6;3;-6)
Другие вопросы по теме Математика
Популярные вопросы
- Можно ли сказать ,что столетия живут в памяти людей.объясните назавите...
3 - Заменить словосочетание построенные на основе примыкания синоничными...
3 - Отцу 41 год, старшему сыну 13лет, дочери 10 лет, а младшему 6 лет....
2 - Из формулы выразить переменную m в) q= cmt...
3 - :цена 1 кг конфет a тенге ,а цена 1 кг яблок b тенге, здесь a b.запишите...
2 - 0.(23)+3,8(5) с решением или ответ не принится...
2 - Вкакую эпоху каменного века был первый зверь ?...
2 - 5примеров со суффиксом ость. 5 примеров со суффиксом ик. 5 примеров...
3 - Сколько символов текста можно передать за 5 секунд,используя модем,...
2 - Найди в отрывке и выпиши слова,которые нельзя разделить на части для...
2
Знайдемо скалярний добуток за до координат:
Знайдемо модулі обох векторів:
Знайдемо кут (позначимо його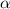 ) зі стандартної формули скалярного добутку:
) зі стандартної формули скалярного добутку:
ответ:аrccos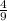
Пошаговое объяснение:
cos (a,b)=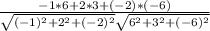 =
=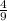
Отже, кут між векторами рівний аrccos