Нужно решить вот такой интеграл.
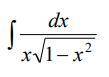
Другие вопросы по теме Математика
Популярные вопросы
- Укажите соответствие между словами и их образования 1.твердь 2.проходят...
1 - Вычислите массу соли, которая образуется при взаимодействии этиламина...
3 - Реши двумя на день рождения катя раздала 24 одноклассникам по 3 шоколадныенфеты...
1 - Запишите и изобразите точками в прямоугольной системе координат первые...
2 - На практической работе учащимся нужно экспериментально доказать амфотерность...
1 - Нравственные качества в произведении мой спутник сочинение...
3 - 200101-168017: 37•23-8239 как решить не понимаю если можно мне в столбик...
2 - Твір на тему війна–трагедія людської долі ...
3 - Подготовить устный ответ на вопрос какова роль пейзажных зарисовок в...
2 - Решить надо 1. із 1000 клітин – попередників статевих клітин – у процесі...
1
Проводим замену:
Получаем: