Нужно решить тригонометрические уравнения
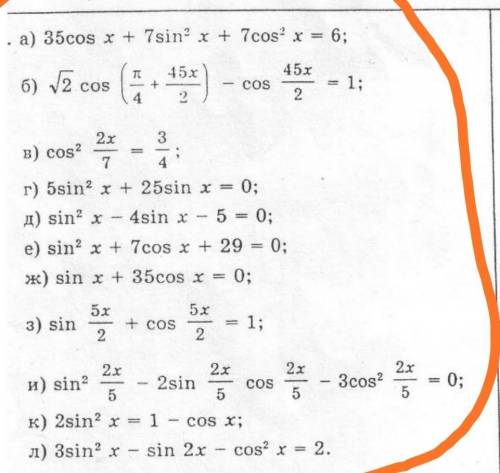
Другие вопросы по теме Математика
Популярные вопросы
- Составьте портрет идеального правителя основываясь на суждениях стародума...
1 - Составить кроссворд со словом символ. нельзя использовать первую букву названия...
1 - Характерний план мирослави і тугара вовка до тексту захар беркут...
1 - Составить предложение со словом градуализм...
2 - Главные герои произведения- дубровский . характеристика. какую роль играет(зачем...
1 - 1.на трех полках лежат книги. на первой полке лежит 42, на второй на 23...
1 - Повсякдене життя української шляхти...
1 - Дано трехзначное число. определить, является ли сумма его цифр кратна 3...
3 - Написать сочинение по картине пластова лето план 1.написать сообщение о...
2 - Составь рассказ о земледельцах в древнем египте нужно...
1
а
n принадлежит Z.
б
n принадлежит Z.
в
г
д
е
ж
з
и
к
л