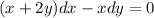 Нужно решить дифференциальное уравнение с разделяющимися переменными. Можете просто подсказать на что поделить чтобы x был в левой части, а у в правой.
Нужно решить дифференциальное уравнение с разделяющимися переменными. Можете просто подсказать на что поделить чтобы x был в левой части, а у в правой.
Другие вопросы по теме Математика
Популярные вопросы
- Определите значение х, при котором значение выражения -3х равно: а)0;...
2 - Нарисуйте схемы строения атомов 1 группы в табл. элементов.напишите...
1 - Сколько кодов можно составить из 9 бит? колько надо бит, чтобы можно...
2 - Что будет если на варёный рис капнуть каплю йода?...
2 - 1. в чем особенность восклицательных предложений? 2. какими бывают...
3 - Опыт по обнаружению органических веществ ( крахмал , белок , жир)....
2 - Произведение чисел 80 и 6 уменьшить на частное 90 и 6...
3 - Сбиологией.мне нужен жизненный цикл мхов! пронумеруйте и обязательно...
1 - Вкаком году была написана картина а.а.пластова летом...
2 - Ошибка у=22-87+27 от меньшего не отнимается большие...
3
Пошаговое объяснение:
Перепишем его немного по-другому:
(x+2y) dx - x dy = 0
(x+2y) dx = x dy
x + 2y = x dy/dx = x*y'
x*y' - x = 2y
x*(y' - 1) = 2y
y' - 1 = 2y/x
Это не уравнение с разделяющимися переменными, а однородное уравнение 1 порядка.
Решается заменой y = u*x; y' = u'*x + u
u'*x + u = 2u + 1
u'*x = u + 1
du/dx = (u+1)/x
du/(u+1) = dx/x
Вот теперь получили разделяющие переменные.
Берём интегралы слева и справа.
ln |u+1| = ln |x| + ln C = ln |Cx|
u = Cx - 1
y = u*x = x(Cx - 1) = Cx^2 - x