Нужно решить 2 из 5 любых диф. уравнения из списка. Ставлю максимальный бал
Если что-то непонятно по цифрам и тд, то спрашивайте. Отвечу сразу!
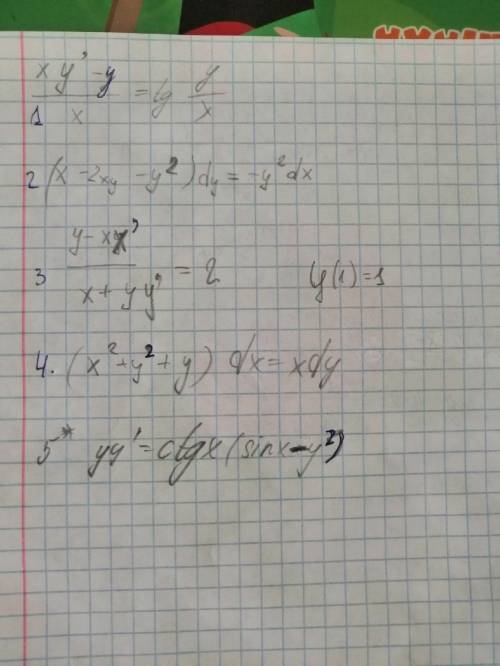
Другие вопросы по теме Математика
Популярные вопросы
- Таблица 1 - ответ бы .Таблица 2 - 5 вариант ....
1 - Путешествие от Касабланки до Триполи какие почвы, население...
2 - Дайте ответ на 1,2,3 очень надо...
3 - Ознаки народної пісні у творі моя любов рожевий квіт...
3 - 30 г жидкости налили в сосуд, площадь дна которого 90 см2. Определите...
3 - Екі тапсырманың бірін орындаңдар Көркем әдебиеттен бастауышқа...
3 - с 6-10,можно все если не трудно)...
1 - Краткий конспект по музыке на тему ОБРАЗЫ СКОРБИ И ПЕЧАЛИ STABAT...
1 - Почему у ножей и ножниц режущие части должны быть остро заточены...
1 - На координатном луче отмечены точкиA(b) иB(4)(рис41).Отметьтена...
2
1.
однородное ДУ
Замена:
константу можно представить в любом виде, для удобства преобразования пишу lnC
общее решение
4.
однородное ДУ
Замена:
общее решение