Нужно подробное решение уравнения
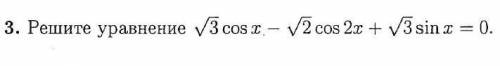
Другие вопросы по теме Математика
Популярные вопросы
- Написать отзыв вессений дождь ...
2 - 4. Чому під час дотикання зарядженого тіла з дрі цього атома?нейтроннезарядженим...
2 - Тәуелсіз елім , тәуелсіз нышандары такырыбына крассворд құрастыру ( 10 сөзден...
2 - Тіло масою 400г упало з висоти 2 м. Знайти швидкість перед самим ударом об...
3 - Відносна густина за воднем деякого газу 8,5. Обчисліть молярну масу цього газу....
1 - Решите надо: Найти площадь заштрихованной фигуры....
1 - Ребят литература 6 класс.Тургенев. Мумудаю 30 б...
2 - 5 Choose the correct words. 1 I never eat any / some crisps.2 I haven t got...
1 - чому Б. Хмельницького вважають одним з найвизначніших діячів в української...
3 - 6-тапсырма, 102-бет Мәтіндегі етістіктерді ауыспалы келер шаққа айналдырып...
2
√3сosx-√2cos²x+√2sin²x+√3sinx=0
√3sinx+√3сosx-√2(cosx-sinx)(cosx+sinx)=0
(cosx+sinx)(√3-√2cosx+√2sinx)=0
cosx+sinx=0;tgx=-1; х=-π/4+πn; n∈Z;
(sinx-cosx)=-√(3/2)
(sinx-sin(π/2-x)=-√(3/2)
2sin(x-π/4)*cosπ/4=-√(3/2);
√2sin(x-π/4)=-√(3/2);
sin(x-π/4)=-√(3/4);
(x-π/4)=(-1)ⁿ⁺¹arcsin√0.75+πк; к∈Z
x=π/4+(-1)ⁿ⁺¹arcsin√0.75+πк; к∈Z
Пошаговое объяснение:
см. изображение