Нужна в решении неопределенных интегралов
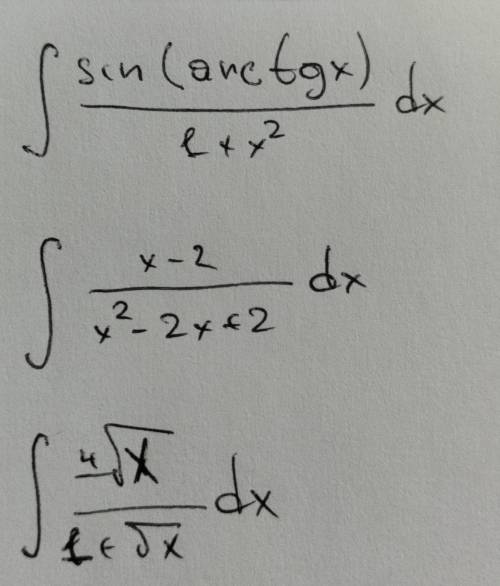
Другие вопросы по теме Математика
Популярные вопросы
- Музыкальные традиции уйгурского народа...
3 - Кто самое опасное животное 21 века?...
2 - Скорость передачи данных по некоторому соединению равна 512000...
2 - Напишите сочинение-миниатюру: „уроки доброты и милосердия в...
3 - Укажіть властивості етанолу, що спричиняють його застосування...
2 - На проволоке длиной 0,7 м подвешен груз массой 20 кг. приподвешивании...
2 - Сокращается ли 9 и 15, если да то на сколько? !...
1 - 3) вычислите площадь квадрата из пункта 2).4) найдите длину...
3 - Твір на тему моральні цінності у творах сучасних письменників...
3 - Write reported questions. example: “who is he? ” she asked....
1
------------------
------------------