НУЖНА Решить систему уравнений из задачника Данко, Попов номер 212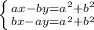
Другие вопросы по теме Математика
Популярные вопросы
- Сколько обращений в тексте о любви Чехов...
1 - Яке правило діє до слова студентство...
3 - Охарактеризуйте методы при которых орден иезуитов ра католичество на белоруских...
1 - Задание:собери из букв 7 названий больших рек или озер Казахстана (букв можно использоватьнеколько...
3 - Пусть . Решите уравнение . Сумма действительных корней уравнения равна …...
3 - Все слова которые содержат в себе буквы - Н,Н,М,А,Р . Любые другие буквы можно добавлять,...
3 - 31. На уроке обсуждали текст «Этикет в разных странах». В хо-де обсуждения ученики...
2 - ОПИСАТЬ одну из трёх картинок (кароче ВПР 7 класс английский)))...
1 - Какая оценка за год если по четвертям 4 3 3 4...
3 - Класс программного обеспечения МS Word...
3
Если а не равно b
то х=(a^2+b^2)/(a-b) y=(a^2+b^2)/(b-a)
если а=b=0 , то х и у любые числа
если а=b и а не равно 0,
то решений бесконечно много , это любая пара х, у, удовлетворяющая соотношению х=у+2а
Пошаговое объяснение:
Первое уравнение
ах-by=a^2+b^2
второе уравнение
bx-ay=a^2+b^2
вычтем из первого уравнения второе.
x*(a-b)+y(a-b)=0
Если а=b последнему уранению удовлетворяют любые х и у.
Вернемся к этому случаю позже. Если это не так, то х=-у
тогда х=(a^2+b^2)/(a-b) y=(a^2+b^2)/(b-a)
теперь рассмотрим случай а=b
(х-у)*а=2a^2
Если а=b =0 решение х и улюбые
Если а не равно 0, то х-у=2а