Нужна определить производные dy/dx формулами дифференцирования.
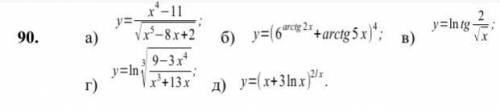
Другие вопросы по теме Математика
Популярные вопросы
- Напишите уравнения возможных реакций между следующими веществами a)нитрат...
2 - Что такое серенада , ,баркаролла,элегия , и кто их исполнял ? ...
2 - Прямая y=2x+b касается графика функции y=x^2+4x+5. a) найдите координаты...
2 - Валюмінійовий посуд налили о,5 л води та 250 г льоду про температурі...
2 - 1. примеры загадки, в которой один предмет называется вместо другого...
2 - Составить диалог на тему 1. өзге тілдің бәрін біл, өз тіліңді құрметте....
2 - Найдите наибольшее значение квадратного трехчлена [tex]-x^{2} -6x+3[/tex]...
2 - Знайдіть невідомі сторони та кути трикутника abc , якщо ab=12см,кут...
1 - Прокололи небо падеж существительного...
2 - Построить график функции : у=(2 в степени х-2)...
2
а
б
в
г
д
по формуле: