нужна .
Нужно решить методом замены неопределенного интеграла
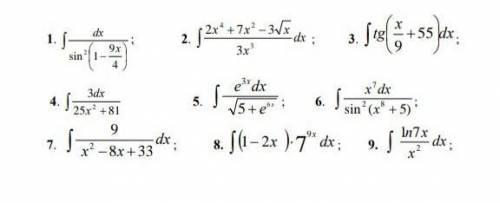
Другие вопросы по теме Математика
Популярные вопросы
- 1 Тапсырма. Сұрақтар мен тапсырмалар. Зерттеушілердің айтуынша: «Шыңғыс...
1 - Х²+х-1≥6 Решите Очень нужно...
2 - Запиши рядом с данными названиями слоёв кожи буквы, соответствующие выполняемым...
1 - Для измерения рН есть различные специальные вещества для определения типа...
1 - Прочитай предложение. Опредили, ошибки какого вида допущены в данном предложении....
2 - Площадь квадрата .Площади равносоставленных фигур 2 .Урок 3. ...
2 - График функции изображен на рисунке. Найти производную этой функции в точке...
3 - Учебные задания Вопросы для самопроверки Вся Монголия и ее население подразделялись...
2 - 1. Сөздерді оқып, жаттап ал. борантүске дейінтүстен кейінбералиерукемпірқосақ...
3 - 5. На площині дані прямі а, b i c.Прямі а i b перетинаються. Чиможуть обидві...
1
1.
2.
3.
4.
5.
6.
7.
8.
По частям:
9.
По частям: