номер если можно с чертежом

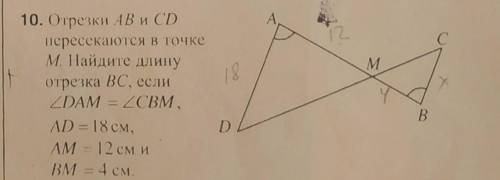
Другие вопросы по теме Математика
Популярные вопросы
- Что ты можешь сказать о судьбах старших троекурова и дубровского?...
1 - задание 2 заполни таблицуа 14см...
2 - 141 2. Определите особенности государства как субъекта гражданских правоотношений....
2 - ask. 1. I... ( could / am able to can sleep for hours when I was a little girl....
1 - Число 60 подати у вигляді суми двох додатних чисел так, щоб сума їх квадратів...
1 - Сульфид меди (ll) массой 84г обработали раствором 350мл 20%-ного раствора соляной...
1 - Петя задумал два числа и написал их произведение. После этого первое из задуманных...
1 - Дана карта природных зон Австралии природные зоны Австралии Назовите виды карты...
1 - Мини-сообщение(4-5 предложений) о кюйши Таттимбете и Курмангазы...
2 - со вторым очень надо умоляю...
1
1. r=2√3 см.
2. l BC l =6 см.
Пошаговое объяснение:
1. По условию одно из сечений проходит через центр шара. В шаре такое сечение наибольшее по площади.
S₁=12*π;
S₂=36=12*3;
π>3 ⇒ 12*π>12*3; ⇒ S₁>S₂.
Сечение S₁ проходит через центр шара. Следовательно S₁ - окружность с радиусом, равным радиусу шара.
S₁=πr², где r - радиус шара;
r=√(S₁/π);
r=√(12π/π)=√12;
r=√12=√(3*4)=2√3 [см].
2 Треугольники AMD и CMB подобные (у этих треугольников равны два соответствующих угла, а именно:
∠АМD=∠CMB, как вертикальные, ∠DAM=∠CMB - по условию.
У подобных треугольников соответствующие стороны пропорциональны.
l AD l : l BC l=l AM l : l MB l;
l BC l =( l AD l*l MB l ):l AM l;
l BC l =18*4/12=(3*6*4)/(6*2)=12/2=6 [см]