Непрерывная функция y=f(x) задана на (-10;6)
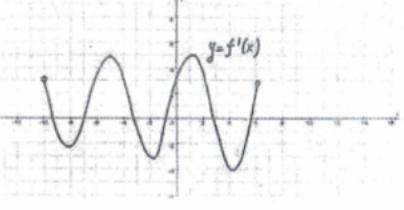
На рисунке изображён график её производной. Укажите количество точек графика этой функции, в которых касательная параллельная оси OX

Для решения данной задачи нужно проанализировать график производной функции f(x). Заметим, что когда производная равна нулю, т.е. производная достигает горизонтальной касательной, график функции f(x) будет параллелен оси OX.

На графике производной видно, что существует одна точка, где касательная параллельна оси OX. Такая точка будет иметь нулевое значение производной функции.

То есть, для того чтобы найти количество точек графика функции f(x), в которых касательная параллельна оси OX, нужно найти количество корней уравнения f'(x) = 0 в интервале (-10;6).

Для этого, нам нужно внимательно проанализировать график производной функции f(x) и узнать, какие значения x соответствуют нулевым значениям производной.

Посмотрим на график:



Мы видим, что на графике есть два корня, приближенно равные -3 и 2.

Таким образом, ответ на задачу: количество точек графика функции f(x), в которых касательная параллельна оси OX, равно 2. То есть, касательная параллельна оси OX в точках x = -3 и x = 2.