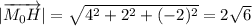Не могу решить ВЫШМАТ вектора
Другие вопросы по теме Математика
Популярные вопросы
- ОЧЕНЬ ! Отметьте и подпишите на координатной прамой точки 4(4,21), B(-4,92)...
3 - Из произведений А.С. Пушкина или Н.В. Гоголя выписать 5-7 предложений...
3 - 3. Побудуй графік функції: 1) y=-2x 2) y=-4 4.Функцію заданою формулою...
3 - Текст на тему Что для меня значат сказки Пушкина...
2 - Придумати три запитання стосовно теми Козацька Слобожанщина та Запорізька...
3 - Выписать определения терминам и привести два примера 1.Океан 2.Материк...
1 - На сколько градусов нагреется кусок свинца,если он упадет с высоты h=26...
1 - Как ты понимаешь слово общее в сказке общее счастье, подбери к нему синоним...
2 - Виконай дії простим -4×(-38)×0,25...
3 - Имеется возможность приобретения недвижимости, выплатив строго фиксированную...
2
2√6
Пошаговое объяснение:
Направляющий вектор данной прямой по каноническому уравнению — это вектор . Запишем данное уравнение в параметрическом виде:
. Запишем данное уравнение в параметрическом виде:
Возьмём некоторую точку H, принадлежащую данной прямой, такую, что вектор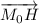 был перпендикулярен вектору
был перпендикулярен вектору 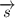 , а значит, и данной прямой. Из параметрического уравнения следует, что точка H имеет координаты
, а значит, и данной прямой. Из параметрического уравнения следует, что точка H имеет координаты 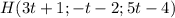 . Тогда вектор
. Тогда вектор  .
.
Поскольку векторы перпендикулярны, их скалярное произведение равно нулю:
Тогда вектор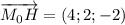 , искомое расстояние есть длина этого вектора:
, искомое расстояние есть длина этого вектора: