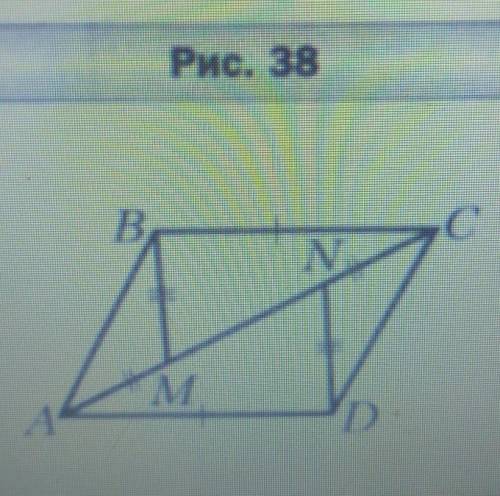
НЕ МОГУ РЕШИТЬ! На рисунке 38 BC = AD, AM = CN, BM = DN. Найдите
угол ABM, ecли угол CDN = 31°​

Для решения данной задачи нам понадобятся знания о свойствах треугольников, а именно о свойстве параллельных прямых и угла между пересекающимися прямыми. На рисунке дано, что BC = AD, AM = CN, BM = DN. Это означает, что сторона BC равна стороне AD, сторона AM равна стороне CN, а сторона BM равна стороне DN. Также известно, что угол CDN равен 31°. Для начала обратим внимание на треугольники AMN и BNC. У них есть две равных стороны AM = CN и BM = DN, а значит, эти треугольники равнобедренные. Из свойств равнобедренных треугольников следует, что углы при основании равны. То есть угол MAN равен углу BNC. Теперь обратимся к треугольнику BMN. У него две равных стороны BM = DN, и угол CDN, одна из сторон угла BNC. По свойству равенства двух углов при неравных сторонах, угол BMN равен углу BNC, а следовательно, угол BMN также равен 31°. Последний шаг заключается в нахождении угла ABM. В этом нам поможет замечание о свойствах параллельных прямых и свойствах угла между пересекающимися прямыми. Из рисунка видно, что отрезки AB и CD параллельны, поэтому угол ABM равен углу CDN. Мы знаем, что угол CDN равен 31°, поэтому угол ABM также равен 31°. Таким образом, ответом на задачу является угол ABM, который равен 31°.