найти значение неопределенного интеграла.
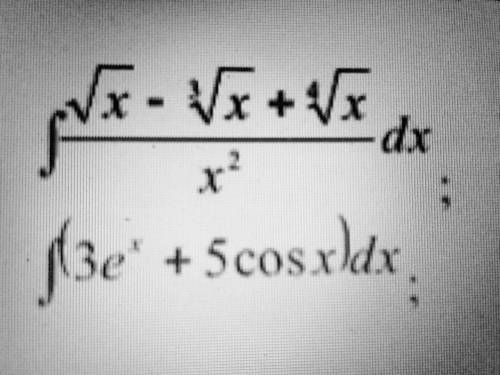
Другие вопросы по теме Математика
Популярные вопросы
- Сан есім зат есімнің қандай мағыналық белгілерін білдіреді? өтінем...
3 - Напишите ионно-молекулярное уравнение nai+hbr=nabr+hi...
1 - 6в кубе плюс 12 в квадрате разделить на 15...
2 - Вмагазине было 7 мешков пшена по 30 кг. продали 180 кг. сколько...
3 - Ребустын шешуі сөз мағынасы əңгіме құрау керек көмек берініздерші...
3 - Раскрыть скобки и : -6(1-ху)-2(3+2ху)+12ху,если х=-2,у=-3...
3 - Признаком четвертичных отложений не является: а) повсеместное...
1 - Втреугольнике cde, dc=5, ce=4, угол c=45. найти de...
1 - Втаблице 3 лишь три вопросы для сравнения но можно придумать и...
3 - Перевидите пожелание другу текст: ! как дела? я тебе желаю здоровья...
1
Пошаговое объяснение:
a ) ∫ [ ( √x - ∛x + ⁴√x )/x²]dx = ∫ [ x^( 1/2 - 2) - x^( 1/3 - 2) + x^( 1/4 - 2) ]dx=
=∫ [ x^( - 3/2) - x^( - 5/3) + x^( - 7/4 )]dx = x^( - 1/2)/( - 1/2) - x^( - 2/3)/( - 2/3) +
+ x^( - 3/4)/( - 3/4) + C = - 2/√x + 3/(2∛x² ) - 4/(3 ⁴√x³ ) + C ;
б ) ∫ ( 3eˣ + 5cosx )dx = ∫ 3eˣ dx + ∫ 5cosx dx = 3eˣ + 5sinx + C .