Найти y' и y'' (производная 1 и 2-го порядка от y)
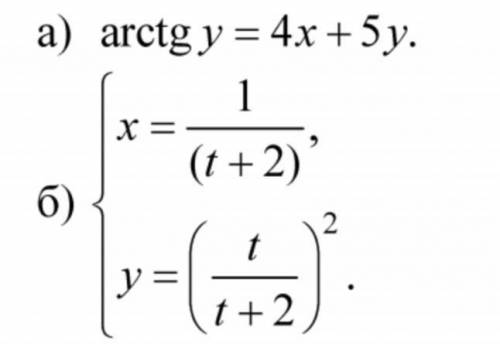
Другие вопросы по теме Математика
Популярные вопросы
- Проверочные слова к словам скольский и к слову автобус...
3 - Какими звуками различаются слова жар и шар...
1 - ответь великий ученый открывший открыл в москве университет...
3 - Размеры помещения прямоугольной формы равны 30м х 24 м. на плане меньшая сторона...
3 - Разобрать по составу слова кораблю, на кораблике, корабельщики, пятёрка, пятнадцать,...
1 - Инфузория туфельки передняя и задняя часть?...
1 - Как повлияло правление бориса годунова на основные сферы жизни общества (, социальную,...
1 - 1)тормозная система автомобиля обеспечивает торможение с максимальным ускорением...
2 - 1.социальная сфера общества зависит от уровня. а) эконом. развитие страны б) полит....
2 - Ребус решите *** умножить на * =*36...
1
а)
представим вместо у' найденную производную первого порядка
б)