Найти все значения параметра K, для которых вершина параболы 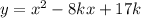 лежит в первом квадранте
лежит в первом квадранте
Другие вопросы по теме Математика
Популярные вопросы
- Отметьте на координатном луче все натуральные числа, которые: а) меньше...
3 - В следующей таблице указан рост учащихся. Назовите их фамилии: а) в порядке...
2 - Какая из точек А и В лежит левее на координатном луче: а) А(1) или В(8);...
3 - От деревни Ивантеево до села Вороново 20 км. Миша шел из Иван-теева до...
2 - Назовите четырехзначное число, которое оканчивается цифрой 1 и которое...
3 - Какая точка лежит левее на координатном луче: а) А(58) или В(60); в)...
2 - От туристского лагеря до города 84 км. Турист ехал на велосипеде из лагеря...
2 - Сколькими можно прочитать слово «знак» на рисунке? Сравните решение этой...
2 - Андрей ехал на автомашине из станицы в город со скоростью 55 км/ч. На...
1 - Купили 3 кг картофеля, 3 кг свеклы, 4 кг моркови, 5 кг яблок, 6 кг капусты,...
1
Пошаговое объяснение:
у=х²-8kx+17k
а=1
b=-8k
c=17k
Вершина параболи лежить в першому квадраті у випадках коли а<0, D>0 або а>0, D<0
Оскільки в даній параболі а=1, тобто а>0, тоді користуємося правилом а>0, D<0
D=b²-4ac=(-8k)²-4*1*17k=64k²-68k=4k(16k-17)
D<0
4k(16k-17)<0
k(16k-17)<0
розвяжемо нерівність
1) →k<0 →k<0 →k∈∅
16k-17>0 k>17/16
2) →k>0 →k>0. →k∈(0; 17/16)
16k-17<0 k<17/16
ВІДПОВІДЬ: при а∈(0; 17/16), вершина параболи лежить в першому квадраті