Найти все значения параметра а при котором уравнение показанное на ФОТО имеет более одного решения на интервале ( 0 ; п/2 )

Найти все значения параметра а при котором уравнение показанное на ФОТО имеет более одного решения н

Ответы

Ega129 15.10.2020 16:11

$a \in \left(-1; - \frac{2}{3}\right) \cup \left(- \frac{2}{3}; - \frac{1}{3}\right)$

Пошаговое объяснение:

Найти все значения параметра а при котором уравнение показанное на ФОТО имеет более одного решения н

ПОКАЗАТЬ ОТВЕТЫ

АлександровнаСаша 15.10.2020 16:11

ответ: a∈(-1;-2/3) ∪ (-2/3 ; -1/3)

Пошаговое объяснение:

ОДЗ: $sin(x) \neq 0$

Используем формулу:

$ctg^2(x) = \frac{1}{sin^2(x)} -1$

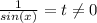
Замена: $\frac{1}{sin(x)} = t\neq 0$

$(1+a)(t^2-1) -(2a+4)t +1-7a = 0\\(1+a)t^2 -(2a+4)t -8a =0$

Заметим, что для того чтобы существовало одно решение на интервале (0;π/2), необходимо и достаточно, чтобы выполнялось условие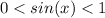 , в этом случае на промежутке (0;π/2) будет существовать ровно ОДНО значение x, в противном случае, решений на данном промежутке не будет.

Откуда, должно выполнятся условие: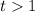

По условию, нужно найти те значения параметра a, при которых будет более одного решения на интервале (0;π/2), а значит данное уравнение должно иметь как минимум два положительных решения.

Рассмотрим линейный случай, ибо может быть бесконечное число решений: a=-1

-2t-8a = 0 - одно решение

2) Основной случай.

Должно быть два корня, каждый из которых больше единицы :

$(1+a)t^2 -(2a+4)t -8a =0\\\frac{D}{4} = (a+2)^2 +8a(1+a) = 9a^2+12a+4 = (3a+2)^20\\ a\neq-\frac{2}{3} \\t_{1} = \frac{a+2+3a+2}{1+a}=41 \\t_{2} = \frac{a+2-3a-2}{1+a} 1\\\frac{-2a}{1+a} 1\\\frac{3a+1}{a+1} < 0\\ \left \{ -1$