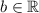Найти все значения a и b, при которых многочлен p_3 (x)=x^3+ax^2-x+b делится на x^2-1.
Другие вопросы по теме Математика
Популярные вопросы
- Придумай и запиши небольшую о путешествии на любую планету солнечной системы....
1 - Хотя бы некоторые . заранее большое ....
3 - Мне надо вопросы на тему природные зоны ответ в одно слово...
3 - Быков писал: интересует в первую очередь не сама война даже неопытный технология...
1 - Разобрать союзы: или, что, если(если и то в одном предложении) то , хотя....
2 - Где тут наречие? доброму везде добро. думай ввечеру, что делать поутру....
1 - Муса джалиль варварство тонкие и толстые вопросы 150...
3 - Установіть хронологічну послідовність подій історії стародавньої греції:...
3 - Вдвумерном массиве действительных чисел найти количество положительных...
1 - Женя максимова подскочила к кате и дёрнула её за руку: - с кем это ты всю...
2
Теорема Безу утверждает, что остаток от деления многочлена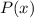 на двучлен
на двучлен  равен
равен 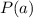 .
.
Данный многочлен делится на (x-1)(x+1). По теореме Безу
Решив как систему уравнений, мы получим a + b =0 откуда a = -b, где