Найти все решения системы уравнений (x; y; z), если x> 0, y> 0, z> 0
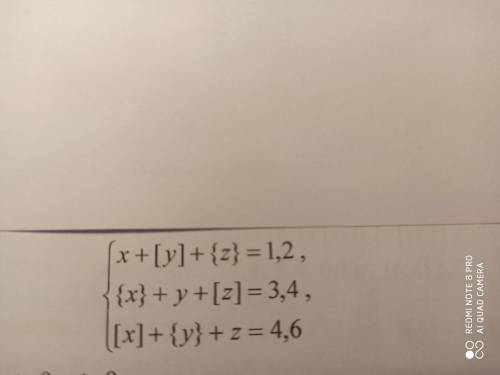
Другие вопросы по теме Математика
Популярные вопросы
- Осуществляет анализ хозяйственно-финансового положения предприятия;...
1 - Основной элемент розничной торговли, когда конкурентами являются...
3 - Расширение возможностей занятости населения и свободный выбор...
3 - Периодические, как правило, традиционные крупные торги, производимые...
2 - Аудит проводится по таким последовательным стадиям 1 < планирование...
1 - Из перечисленных организационно-правовых форм малого предпринимательства...
3 - Услуги, направленные на оказание содействия покупателю и продавцу...
3 - Совокупность видов предпринимательской деятельности, увеличивающая...
1 - При совершении биржевой сделки обязательному оглашению подлежат...
1 - Долговая несостоятельность, отказ предпринимателя платить по...
1
x + [y] + {z} = 1,2
{x} + y + [z] = 3,4
[x] + {y} + z = 4,6
Если сложить все три уравнения, то получится по одному слагаемому x, y и z + их целые и дробные части. Целая + дробная часть равна самому числу. Поэтому получится 2x + 2y + 2z = 9,2, или x + y + z = 4,6.
Приравняем это к третьему уравнению:
x + y + z = [x] + {y} + z = 4,6
x + y = [x] + {y} = 4,6
{x} + [y] = 4,6
С другой стороны, 4,6 = 1,2 + 3,4, то есть
{x} + [y] + x + y + z = 4,6
Но x + y + z = 4,6, значит {x} + [y] = 0.
Т.к x > 0 и y > 0 и z > 0, то
{x} = 0
{x} - целое число
[y] = 0
0 < y < 1
Из первого уравнения системы:
x + [y] + {z} = 1,2
Но [y] = 0, поэтому
x + {z} = 1,2
[x] + {x} + {z} = 1,2
{x} = 0, поэтому
[x] + {z} = 1,2
Т.к x > 0 и y > 0 и z > 0, то x = 0 или 1.
0 не может быть, т.к {z} < 1.
Значит [x] = 1 и x = 1, а {z} = 0,2
Из второго уравнения системы:
{x} + y + [z] = 3,4
y + [z] = 3,4
Т.к [y] = 0, то y = 0,4, а [z] = 3.
Все переходы равносильные, поэтому решение единственное
ответ: (1, 0,4, 3,2)