Найти все решение в целых числах x, y, z системы двух уравнений
x+y+z=3, x^3+y^3+z^3=3
Другие вопросы по теме Математика
Популярные вопросы
- Назовите вещество по международной номенклатуре...
2 - XIII гасырдагы монгол шапкыншылығы картасын пайдаланып, тапсырманы...
3 - Test. 8 form №1. Read the text and decide if each sentence...
2 - Головні релігійні центри України.Главные религийные центры Украины....
2 - Все лето листья подставляли солнцу свои ладошки и щечки,спинки...
1 - Твір на тему китайськапоезія. Чим подобається?...
3 - Решите уравнение х÷5 -100÷5=100...
2 - 1. До яких типів хімічних реакцій за різними ознаками можна...
3 - хто знает или найдите в инете может кто проходит морофон по...
3 - 1. Визначте, що з переліченого нижче є фізичним явищем: а) прокисання...
3
Пошаговое объяснение:
Из уравнения
следует, что среди чисел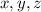 либо все нечетные, либо одно.
либо все нечетные, либо одно.
Заметим, что
Из нашего условия это преобразуется как
Но мы знаем, что среди чисел либо все четные, либо одно. Если четны все, то они могут быть равны только
либо все четные, либо одно. Если четны все, то они могут быть равны только 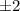 в этом случае числа
в этом случае числа 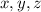 могут быть равны с точностью до перестановки только
могут быть равны с точностью до перестановки только 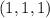 или
или 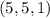 . Второе решение не подходит в исходное уравнение, поэтому его отметаем. Если же среди чисел
. Второе решение не подходит в исходное уравнение, поэтому его отметаем. Если же среди чисел  только одно четное, то оно обязано быть равно
только одно четное, то оно обязано быть равно 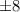 , а остальные -
, а остальные - 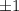 . В этом случае
. В этом случае 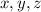 равны
равны 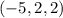 ,
, 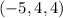 ,
, 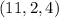 . Из этих троек нам подходит только вторая.
. Из этих троек нам подходит только вторая.
В итоге, решений всего два.