Найти указанный предел, используя второй замечательный предел
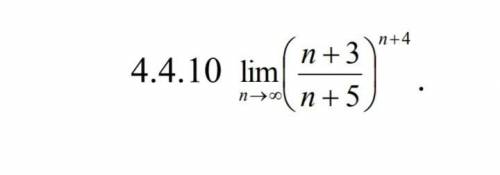
Другие вопросы по теме Математика
Популярные вопросы
- . ПАО Русский дом в январе 2017 года продало ООО Фаворит теплоход. Передача...
2 - краткое содержание СНЕЖНАЯ КОРОЛЕВА ЧЕТКО И МОЖНО 5-6 ПРЕДЛОЖЕНИЙ...
3 - Как повлияла любовь к Маше на Владимира Дубровского? Какие ключевые слова...
2 - Иннокентий составляет семибуквенные слова из букв Е, И, Й, К, Н, О, Т. Сколько...
2 - Відредагуйте подані словосполучення. Не повторюйте таких помилок ні в усному,...
1 - 161а.Что представляют собой гетерогенные химические системы и их разновидности,...
3 - Назвіть газ, підвищення концентрації якого активує дихальний центр...
3 - Б. Запишите предложения, найдите обособленные обстоятельства, подчеркните...
3 - Длина прямоугольника 52 см, а ширина составляет 1/4 от длины. На сколько сантиметров...
1 - Особенности стиля Пикассо и Брака...
2
Второй замечательный предел гласит:
\[ \lim_{{x \to 0}} \frac{{\sin(x)}}{x} = 1 \]
В нашем случае, чтобы применить этот предел, преобразуем выражение, чтобы оно соответствовало форме второго замечательного предела.
Посмотрим на данный предел и заметим, что какое-то число умножается на \(\frac{1}{x}\):
\[ \lim_{{x \to 0}} 2x \cdot \frac{{\sin(5x)}}{{5x}} \]
Мы знаем, что \(\frac{{\sin(5x)}}{{5x}}\) - это искомая функция, которую нужно заменить на \(1\). Значит, можем записать предел в следующей форме:
\[ \lim_{{x \to 0}} 2x \cdot 1 \]
А так как умножение на \(1\) не меняет значения, то можно записать:
\[ \lim_{{x \to 0}} 2x \]
Теперь, чтобы вычислить предел, просто подставим \(0\) вместо \(x\):
\[ 2 \cdot 0 = 0 \]
Ответ: указанный предел равен \(0\).