1. Математика
  2. Найти указанные неопределенные

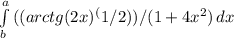
Найти указанные неопределенные интегралы и результаты интегрирования проверить дифференцированием: \int\limits^a_b {((arctg (2x)^(1/2))/(1+4x^2)} \, dx\int\limits^a_b {(x^3-4)/(x^2+6x+9)} \, dx ^


Найти указанные неопределенные интегралы и результаты интегрирования проверить дифференцированием:

Lelka8891 Lelka8891    3   21.06.2021 21:02    0

Ответы
21032008 21032008  21.07.2021 22:05

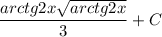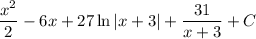ОТВЕТ: 1) \dfrac{arctg2x\sqrt{arctg2x}}{3}+C; 2) \dfrac{x^2}{2}-6x+27\ln |x+3|+\dfrac{31}{x+3}+C.

Пошаговое объяснение:

1) Сделаем замену:

t=arctg2x\Rightarrow dt=\dfrac{2dx}{1+4x^2}. Получаем интеграл:

\int\dfrac{\sqrt{t}}{2}dt=\dfrac{1}{2}\int t^{\frac{1}{2}} dt= \dfrac{1}{2}\cdot\dfrac{t^\frac{3}{2} }{\frac{3}{2} } +C=\dfrac{t\sqrt t}{3}+C=\dfrac{arctg2x\sqrt{arctg2x}}{3}+C.

2) Максимально упростим дробь. Выделим целую часть:

\dfrac{x^3-4}{x^2+6x+9}=\dfrac{x^3+6x^2+9x-(6x^2+36x+54)+27x+50}{x^2+6x+9}=\\\\=\dfrac{x(x^2+6x+9)-6(x^2+6x+9)+27x+50}{x^2+6x+9}=x-6+\dfrac{27x+50}{(x+3)^2}.

Упростим полученную дробь. Запишем её в виде суммы двух дробей вида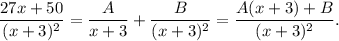 \dfrac{27x+50}{(x+3)^2} =\dfrac{A}{x+3}+\dfrac{B}{(x+3)^2}=\dfrac{A(x+3)+B}{(x+3)^2} .

Первая и последняя дроби с равными знаменателями равны - соответственно, равны их числители:

27x+50=Ax+3A+B, откуда

\begin{cases}A=27,\\3A+B=50\end{cases} \Rightarrow \begin{cases}A=27,\\B=-31.\end{cases}

Окончательно интеграл можем записать в виде суммы табличных интегралов:

\int\dfrac{x^3-4}{x^2+6x+9} dx=\int(x-6+\dfrac{27}{x+3}-\dfrac{31}{(x+3)^2})dx=\dfrac{x^2}{2}-6x+27\ln |x+3|+\dfrac{31}{x+3}+C.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
алибек29 алибек29  01.08.2019 20:20
Отрезок соединяющий противоположные вершины прямоугольнника...
Marksensei Marksensei  01.08.2019 20:20
Зачем противогазу хобот (шланг) вопрос мучает меня и давайте отвечать без шуток) )...
stazagreen stazagreen  01.08.2019 20:20
Язадумал число прибавил к нему 1,5 сумму разделил на 4,8 к результату прибавил 9,5.из суммы вычел 4,8 получилось 7,2.найдите число которое я задумал...
elenaelena6 elenaelena6  01.08.2019 20:20
Точки d,c и e лежат на отрезке ab . точка d середина отрезка ac , а точка e середина отрезка cb. расстояние между точками d и e равно 16 см . наидите длину отрезка ab...
dashasergeeva10 dashasergeeva10  01.08.2019 20:20
Найдите корни уравнения 9х^2-10х+1=0...
acononencko201 acononencko201  01.08.2019 20:20
Cо школьного участка собрали 48 кг моркови и лука,морковь составляет 65%всех собранных овощей а остальные лук.сколько лука собрали с участка?...
denholopДанила23231 denholopДанила23231  01.08.2019 20:20
Реши . участок квадратной формы с длиной стороны 30 м засеяли морковью.сколько граммов семян потребовалось. если на 10 кв.м участка использовали 15г семян?...
CloudySun CloudySun  01.08.2019 20:20
Решить : на станции технического обслуживания 3 механика отремонтировали за месяц 78 автомобилей 1 механик отремонтировал в 1 с половиной раза больше автомобилей чем 2...
Raf4ik15 Raf4ik15  01.08.2019 20:20
Как решить нужно разделить чтобы каждый был по 6 метров а веревка 16 метров...
maksborovkov20oxdws5 maksborovkov20oxdws5  01.08.2019 20:20
Запишите на языке число m на 8 больш числа n...

Популярные вопросы