Найти точку минимума функции y = x^x
Другие вопросы по теме Математика
Популярные вопросы
- Отгадать слово из 7 букв и- о- н -е встречающиеся в живой природе...
3 - Произвести синтаксический разбор предложения: с осени запаслись желудями,шишками,семенами,вениками....
1 - Какие системы органов образуются из эктодермы,мезодермы и энтодермы...
3 - Загадка-дві дощечки, дві сестрт несуть мене з гори...
3 - Окосмосе мечтает слон.у космонавтах на примете,поднять ракету может он- но...
2 - Найди значения произведений 15: 5 5х4 6: 2 используй полученные равенства,...
1 - Пусть a= эта ночь звездная , а в = эта ночь холодная . выразите следующие формулы...
3 - Скласти речення про лисицю і зайця за схемою _ _ , а _ _ ....
1 - )запишите для бутанола-2 уравнения реакций взаимодействия с натрием, бромоводородом,...
3 - Проверочное слово к слову деформация на первый слог...
2
ответ: 1/е
Пошаговое объяснение:
ОДЗ х∈(0;+∞);
прологарифмируем обе части, они положительны, ㏑у=㏑(x^x);
㏑у=х㏑(x);
возьмем производную от обеих частей.
у'/y=㏑x+x/x
y'=(㏑x+1)*y;
y'=(㏑x+1)*(x^x); x^x≠0;
y'=0, если ㏑x+1=0, ㏑x=-1⇒х=е⁻¹; х=1/е
установим знаки, при переходе через критическую точку 1/е;
___01/е
- +
поэтому х=1/е- точка минимума.
ответ: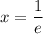 .
.
Найдём стационарные (критические) точки.
Знаки y':
Так как производная меняет знак c минуса на плюс, то имеем точку минимума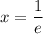 .
.