Найти точки перегиба функции y=x/x^2-1
arinashabalina1
1
13.11.2020 15:56
2
Ответы
san31032009
13.12.2020 15:57
![y=\dfrac{x}{x^2-1}\ \ ,\ \ \ ODZ:\ \ x\ne \pm 1\ ,\\\\\\y'=\dfrac{1\cdot (x^2-1)-x\cdot 2x}{(x^2-1)^2}=\dfrac{-x^2-1}{(x^2-1)^2}=-\dfrac{x^2+1}{(x^2-1)^2}\\\\\\y''=-\dfrac{2x(x^2-1)^2-(x^2+1)\cdot 2(x^2-1)\cdot 2x}{(x^2-1)^4}=\\\\\\=-\dfrac{2x\, (x^2-1)\cdot \Big((x^2-1)-2(x^2+1)\Big)}{(x^2-1)^4}=-\dfrac{2x\, (-x^2-3)}{(x^2-1)^3}=\dfrac{2x\, (x^2+3)}{(x^2-1)^3}=0\\\\\\\\znaki\ y'':\ \ \ ---(-1)+++[\, 0\, ]----(1)+++](/tpl/images/1476/3961/af69b.png)
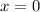- абсцисса точки перегиба, при переходе через точку О(0,0) функция меняет вогнутость на выпуклость, т.к. знак у'' меняется с (+) на (-) .
Другие вопросы по теме Математика
vinchez1
23.08.2019 05:10
SuperDusia
23.08.2019 05:20
00Рахат00
23.08.2019 05:20
nikitasolyny
23.08.2019 05:20
krasio
23.08.2019 05:20
Tania22012003
23.08.2019 05:20
anna20032004
23.08.2019 05:20
Lizzik657
23.08.2019 05:20
Популярные вопросы
- Укажите строку(-и), в которой(-ых) в обоих словах пишется разделительный...
2 - 4 Write a phrasal verb from the box in each gap. get back. get up go...
1 - 1 Вычислить log^2 5-log ^10+2 log^5 25 А) 16log^3 2 2 Б) В) 0,5 Г) 3...
2 - Put the verb in brackets into the past perfect or the past perfect continuous....
3 - Put the verb in brackets into the correct past form...
2 - Розкладіть на множники (а²+b²)²-4a²b²...
1 - На входе трехфазной цепи поданы линейные напряжения Uab=Ubc=Uca=Uл=390В....
2 - Put the verb in brackets into the past simple or the past perfect.State...
2 - 9. Сила тяжести, действующая на тело, 23 Н. Чему равна масса тела? а)...
1 - в решении математического задания...
1