Найти tg\alpha , если 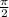 <
< 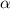 <
< 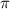 и sin
и sin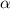 =
= 
Другие вопросы по теме Математика
Популярные вопросы
- Постройте 2 произвольных отрезка симметричные оси симметрии КМ...
3 - Хлопчик везе свого друга на санчатах по горизонтальній дорозі, прикладаючи...
3 - Очень класс Номер 1. Из предложенного ниже перечня выберите две пары веществ,...
2 - все которые у меня есть) 7 класс, геометрияидет контрольная...
2 - даю 10 сори что мало балов английский , умаляю и главное правильно самое...
2 - В трапеции АВСD ∠A = 90°, ∠D = 45°, BC = 6 см, AB = 14 см. Найдите AD. ответ...
1 - Если экономика, функционирующая в условиях полной занятости, переживает отрицательный...
2 - Оцініть якість трудових ресурсів в Україні. Яке значення має якість трудових...
1 - СОЧ по алгебре ребят , что знаете( даю)...
1 - Який виграш у силі дає така система? З якою силою треба тягнути за вільний...
2
(см. объяснение)
Пошаговое объяснение:
По определению:
Из основного тригонометрического тождества с учетом того, что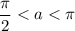 , следует:
, следует:
Тогда:
Подставим значение синуса из условия в формулу:
Задание выполнено!
Замечу, что можно было воспользоваться готовой формулой:
Откуда бы получили:
И, очевидно, что положительный корень посторонний.