1. Математика
  2. Найти такие значения а , для

Найти такие значения а , для которых корни уравнения Log(2) ( x+3) -2 Log(4) x= a
были бы расположены между числами 3 и 4

alino4kakostina alino4kakostina    2   07.07.2021 22:31    1

Ответы
Danil185071 Danil185071  06.08.2021 23:03

\log_2(x+3)-2\log_4x=a\\

ОДЗ: x-3

\log_2(x+3)-2\log_4x=\log_2(x+3)-2 \cdot \dfrac{1}{2}\log_2x=\\=\log_2(x+3)-\log_2 x=\log_2 \dfrac{x+3}{x}=\log_2 \left(1+ \dfrac{3}{x}\right)=a\\2^a=1+\dfrac{3}{x}\\ \\2^a-1=\dfrac{3}{x}\\\dfrac{1}{2^a-1}=\dfrac x3\\\\ x=\dfrac{3}{2^a-1}\\3

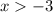
Здесь можно уже не использовать сложные преобразования, а внимательно всмотреться в выражение по-центру. Оно будет больше единицы при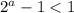 2^a-1, то есть 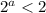2^a. В силу монотонности показательной функции:

2^a

Нашли верхнюю границу a.

Рассмотрим неравенство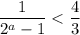 \dfrac{1}{2^a-1} . Поскольку 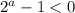2^a-1 в силу 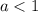a, мы можем перемножить крест-накрест, изменив при этом знак:

4(2^a-1)3\\2^a-1\dfrac{3}{4}\\2^a\dfrac{7}{4}\\a\log_2\dfrac{7}{4}

Нашли нижнюю границу a.

a \in \left(\log_2 \dfrac{7}{4} ; \,1\right).

Проверка решения на скриншотах (если вы понимаете, почему там именно так записано, то есть умеете проверять решения с программ для построения графиков).


Найти такие значения а , для которых корни уравнения Log(2) ( x+3) -2 Log(4) x= a были бы расположен
Найти такие значения а , для которых корни уравнения Log(2) ( x+3) -2 Log(4) x= a были бы расположен
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
maha80 maha80  29.05.2019 00:20
Докажите, что число расставить на доске 8 ферзей так, чтобы они не били друг друга – четно....
rsdgdddddddddddd rsdgdddddddddddd  29.05.2019 00:20
А)саша покупал 3 одинаковых блокнота. когда продавец назвал их общую стоимость 158р. саша подумал: видимо продавец ошибся -и попросил пересчитать. кто прав: продавец или саша?...
micser2017 micser2017  29.05.2019 00:20
Начертить фигуры площадь которых ровна 4 квадратных см: 6 квадратных см; 8квадратных см...
Andrew1712 Andrew1712  29.05.2019 00:20
Это пример! 90259+792*9-4830: 5= надо указать действие,и ответ ....
Даша12Няшка Даша12Няшка  29.05.2019 00:20
Цена 1кг конфет 215р.50к. в ящике 4 кг этих конфет. какова стоимость конфет,лежащих в ящике?...
SSultanShaS SSultanShaS  29.05.2019 00:20
Обчисли площу поверхні прямокутного паралелепіпеда, довжина якого дорівнюють: 1) 5см, 3см і 2см 2) 3 дм, 4дм і 7 дм...
кузя1310 кузя1310  29.05.2019 00:20
На элли в пещеру прибыли правители волшебной страны со свитой из 100 человек.пятую часть свиты составляли жевуны,десятую часть оставшихся-мигуны,а остальные,дуболомы.сколько...
Lngtnk5 Lngtnk5  29.05.2019 00:20
Які почуття очі, якщо вони: розбігаються? блищать? загорілися? пропікають наскрізь? метають іскри?...
zyzae zyzae  29.05.2019 00:20
Усергея был аквариум основа каторого -квадрат со стороной 50 см. уровень воды в нём составляет 32 см.мальчику купили новый аквариум длина дна 80см а ширина 40 см. мальчик...
gpatimat gpatimat  29.05.2019 00:20
Решите уравнения 1)х-17=17 2)3,5+у=-3,5 3)3х-7=-7 4)5(у-2,4)=35 5)х: (4,2)=7 6)(3+0,5х)*(-0,6)=12...

Популярные вопросы