Найти сумму ряда где n-ый член задан как n! * n
Нужно решение.
Другие вопросы по теме Математика
Популярные вопросы
- подалуйста :{ 1.Риси характеру Діка Сенда. 2.Поведінка Діка Сенда...
1 - Упражнение 5, стр. 113.6 класс Прочитай текст. Сформулируй два...
3 - с алгеброй и обьяснение краткое и легкие решить 1. Найдите корни:...
3 - Определите заряд ядра порядковый номер элемента...
3 - Конденсатор якої ємності треба ввімкнути в коливальний контур...
1 - 29299×83393:5+3939383838384482-292929293 кто это реально решит...
2 - В какие точки перейдут точки(1;2),(0;2),(2;2)при симметрии относительно...
1 - Значение цитаты На пкти к единовластию . История Древней Руси....
1 - Поло 16. Определите, какая гласная пишется перед суффиксом -вш-....
3 - Выберите 2 области с более высокой долей населения: Забайкальский...
3
Пошаговое объяснение:
По определению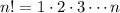
Тогда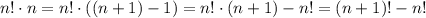
Значит, ряд можно переписать в виде
Все слагаемые, кроме первого и последнего, сокращаются.