1. Математика
  2. Найти сумму корней многочлена

Найти сумму корней многочлена х^5-5x^4-9x^3+41x^2+32x-60

спайки5 спайки5    3   21.09.2019 17:36    7

Ответы
demeshkin1 demeshkin1  08.10.2020 07:37

Разложим на множители многочлен. Есть и разные решить по Безу, схеме Горнера.

x^5-5x^4-9x^3+41x^2+32x-60=x^5-5x^4-(9x^3-45x^2+4x^2-\\ \\ -20x-12x+60)=x^4(x-5)-(x-5)(9x^2+4x-12)=\\ \\ =(x-5)(x^4-9x^2-4x+12)=(x-5)(x^2(x-3)(x+3)-4(x-3))=\\ \\ =(x-5)(x-3)(x^3+3x^2-4)=(x-5)(x-3)(x^3+2x^2+x^2+2x-\\ \\ -2x-4)=(x-5)(x-3)(x^2(x+2)+x(x+2)-2(x+2))=\\ \\ =(x-5)(x-3)(x+2)(\underbrace{x^2+x-2}_{(x-1)(x+2)})=(x+2)^2(x-1)(x-3)(x-5)

Корни многочлена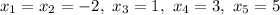 x_1=x_2=-2,~ x_3=1,~ x_4=3,~ x_5=5

Сумма корней многочлена: -2 - 2 + 1 + 3 + 5 = 5

ПОКАЗАТЬ ОТВЕТЫ
GanyaOle GanyaOle  08.10.2020 07:37

ответ и решение во вложении


Найти сумму корней многочлена х^5-5x^4-9x^3+41x^2+32x-60
Найти сумму корней многочлена х^5-5x^4-9x^3+41x^2+32x-60
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
imamverdueffsa imamverdueffsa  22.01.2022 09:22
К бассейну проведены три трубы. Если по первой и второй трубе вода в бассейн поступает, то через третью трубу вода сливается. Первая труба наполняет бассейн за 6 часов, вторая...
08760000 08760000  22.01.2022 09:22
Доброе утро задача на двух участках общей площадью 240 м2 весной высадили рассаду огурцов на каждом квадратном метре высаживали одинаковое количество кустиков на одном участке...
СветланаУсова СветланаУсова  22.01.2022 09:20
Ребят с экономикой, задача...
viteralinap06rap viteralinap06rap  22.01.2022 09:17
1) При каком х выражение 1,5х-2 равно выражению х -9 ?. 2) При каком у выражение 5-3у больше выражения 2у -3 на 7 3) При каком х выражение х-3 больше выражения 2х-1,5 в 3 раза...
поварешка1 поварешка1  22.01.2022 09:16
2. а) Рассмотри график движения. ответы на вопросы: 1) Какое расстояние было между автомобилем и велосипе- истом в начале пути? 2) Через сколько часов они встретились? 3) Какова...
Ilyasha311 Ilyasha311  22.01.2022 09:15
Определи уравнения, у которых нет корня и только один корень. Верных ответов: 3 |-x + 10 - 20| + 1/4 = 0,25 |-(-)(-)(-) • z - 1| - 2 = 0 |-x-1-1-1| = -1 |-n +1+1+1+1| = 1 |-m|+12=...
алмаз122 алмаз122  22.01.2022 09:15
А1. Объем комнаты равен 105 м3. Длина комнаты 7 м, ширина 5 м. Найдите высоту комнаты. 1) 2м 2) 3 м 3) 4м 4) 3 м2 А2. Найдите объем прямоугольного параллелепипеда, изображенного...
СанаевАнтон СанаевАнтон  22.01.2022 09:14
через первую трубу водоём можно наполнить за 6 часов а вторую за 1цел. 1/3от времени первой за сколько они наполнятся за сколько часов наполнится водоём при совместной работе...
shulgavitaliy1ozo6g1 shulgavitaliy1ozo6g1  22.01.2022 09:14
Ширина прямоугольника на 6 см меньше его длины.найди периметр и площадь,если ширина составляет 4/5 длины задача есть еще в фото...
sashagrachev0 sashagrachev0  22.01.2022 09:14
Вырази в центнерах 7т 400кг...

Популярные вопросы