1. Математика
  2. Найти сумму координат точки

Найти сумму координат точки с отрицательной абсциссой, касательная в которой к графику функции 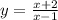y=\frac{x+2}{x-1} параллельна прямой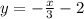 y=-\frac{x}{3} -2

Djzhdujd Djzhdujd    3   13.07.2021 16:51    2

Ответы
Nikitos235555555555 Nikitos235555555555  12.08.2021 17:59

Угловой коэффициент касательной равен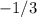 -1/3, а значит, производная в искомой точке будет равна -1/3:

f'(x_0)=-1/3

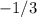Найдём производную:

f'(x)=\dfrac{(x+2)'(x-1)-(x+2)(x-1)'}{(x-1)^2}=\dfrac{x-1-(x+2)}{(x-1)^2}=\dfrac{-3}{(x-1)^2}.

\dfrac{-3}{(x-1)^2}=-\dfrac{1}{3}\\\dfrac{3}{(x-1)^2}=\dfrac{1}{3}\\(x-1)^2=9\\

Тут не нужно раскрывать скобки, поскольку слева и справа — полный квадрат. Нам нужно только отрицательное решение, поэтому:

(x-1)^2=(-3)^2\\x-1=-3\\x=-2

f(-2)=\dfrac{-2+2}{-2-1}=0

Получили точку с координатами –2 и 0. Их сумма –2.

ответ: –2.

На скриншоте проверка на компьютере. К этому графику есть ещё одна касательная, но она не подходит по условию (обозначил пунктиром — не надо перерисовывать).


Найти сумму координат точки с отрицательной абсциссой, касательная в которой к графику функции пара
ПОКАЗАТЬ ОТВЕТЫ
Dogi2008 Dogi2008  12.08.2021 17:59

Пошаговое объяснение:

у нас дана прямая с угловым коэффициентом у =(-1/3)х-2 .

любая ║ ей прямая будет иметь такой же угловой коэффициент -1/3

для случая касательной угловой коэффициент - значение производной в точке касания. значит, найдем производную - найдем точку касания

\displaystyle y'=\bigg (\frac{x+2}{x-1}\bigg )'=\frac{(x+2)'(x-1)-(x+2)(x-1)'}{(x-1)^2} =-\frac{3}{x^2-2x+1}

теперь y'(x₀)= -1/3

\displaystyle -\frac{3}{x^2-2x+1} =-\frac{1}{3} \\\\9=x^2-2x+1\\\\x^2-2x-8 = 0 \qquad \Rightarrow \quad x_1=-2,\quad x_2=4

точка х₂ = 4 нас не интересует.

найдем точку касания с отрицательной абсциссой

у(-2) = 0, т.е. точка (-2; 0)

ответ

сумма координат точки с отрицательной абсциссой (-2; 0) равна (-2)

дополнительно можно найти уравнение касательной

\displaystyle y_k=-\frac{1}{3} x -\frac{2}{3}

проверим всё на чертеже


Найти сумму координат точки с отрицательной абсциссой, касательная в которой к графику функции пара
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
dasha18s10 dasha18s10  02.08.2019 06:20
Ввдоль улице на одинаковом расстоянии друг от друга посажены 17 деревьев. расстояние между крайними деревьями 64 метра. на каком расстоянии друг от друга посажены деревья?...
ejjekskaksk ejjekskaksk  02.08.2019 06:20
Ученик задумал увеличел его в 1целую 5 6-ых раза прибавил в 2 целых 3 и получил 7 целых 8 какое число он задумал...
vlad199411003 vlad199411003  02.08.2019 06:20
Автостоянке всего 38 из них 2целых1/6 больше легковых машин ,сколько на стоянке грузовых машин...
3339991 3339991  02.08.2019 06:20
За первый час автобус за второй-35% расстояние от деревни до города,а за третиц-70км. каковл расстояние от деревни до города?...
SMILЕ31 SMILЕ31  02.08.2019 06:20
Втреугольнике мкс сторона мк на 8 см больше стороны кс найдите сторону мс если периметр равен 59 см а сторона кс равна 14 см...
sofia0lord0dominator sofia0lord0dominator  02.08.2019 06:20
Вфермерском хозяйстве 3/5 всего поля засеяли пшеницой,а 7/20 поля засадили овощами.площадь поля,засеянного пшеницей,на 17 га больше площади поля, занятого овощами.найдите площадь...
kirilladmiiral kirilladmiiral  02.08.2019 06:20
Нужно решить уровнением #69 ученик задумал число,увеличил его в одну целую пять шестых раза,прибавил 2,3 и получил 7,8.какое число он задумал #70 из кувшина отлили одну третью...
antonareninozvuw8 antonareninozvuw8  02.08.2019 06:20
Сократите дробь рациональным числитель,5/6*0,14*5,4*0,3 -знаменатель, с объяснением...
ValeraShara ValeraShara  02.08.2019 06:20
Сама , арман и дархан втроем собрали 78 марок . армап собрал в 3 раза больше , а дархан -2,5 раза больше , чем санат . сколько марок собрал санат? сколько марок собрал дархан?...
mriya1987 mriya1987  02.08.2019 06:20
Вкниге 75 страниц. в первый день ученик прочитал 3/5 всей книг , во второй - 2/5 остатка . сколько страниц ему осталось прочитать ?...

Популярные вопросы