Найти сумму коэффициентов a+с квадратного трехчлена ax2+2x+c, если x=2 и x=-4, корни данного трехчлена.

Поскольку известны корни трехчлена, то верны следующие равенства:

Преобразовываем оба уравнения:

Вычитаем второе из первого:

Приводим подобные:

, отсюда

Подставляем a в одно из уравнений, например, в первое:

, откуда

Тогда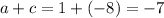

По теореме Виета, для квадратного уравнения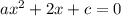 , если 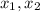- корни уравнения, то верно следующее:

(правая часть первого уравнения - коэффициент при x, деленный на коэффициент при старшей степени, т.е. a, взятый со знаком минус, правая часть второго уравнения - свободный коэффициент, то бишь c, деленный на коэффициент при старшей степени, то бишь a)

Поскольку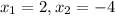 , то получаем:

Из первого уравнения находим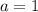 . Подставляем a во второе уравнение, находим, что 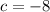. Наконец, находим сумму:

Эпилог

Двумя получили одинаковый результат, и это хорошо.