Найти решение задачи Коши.
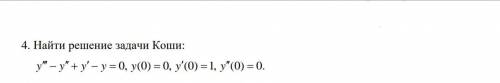
Другие вопросы по теме Математика
Популярные вопросы
- Автоколонна длиной 200 м и встречный автомобиль имеют равные скорости. С какой...
1 - В кино показывают следующий трюк. Поезд идет со скоростью 20 м/с, а по платформе...
2 - Поезд длиной 240 м, двигаясь равномерно, въезжает на мост. С того момента, когда...
1 - Чтобы успеть отбежать от места взрыва заряда, применяют бикфордов шнур, по которому...
3 - На рисунке изображен график, характеризующий полет птицы. Сколько времени летела...
1 - Докажите что расстояние от точки B до прямой HM равно расстоянию между прямыми...
2 - На горизонтальном участке пути автомобиль ехал со скоростью 72 км/ч в течение...
2 - Человек полпути проехал на велосипеде со скоростью 25 км/ч, а остаток пути со...
2 - Турист за 25 мин км, затем полчаса отдыхал, а потом пробежал еще 800 м за 5 мин....
3 - Два автомобиля выехали одновременно из города и двигались по одной и той же прямой...
2
общее решение
система:
частное решение