1. Математика
  2. Найти производные заданной функции

Найти производные заданной функции y=3^x×tgx

ksuholina ksuholina    3   01.10.2019 06:30    1

Ответы
ressoli444 ressoli444  21.08.2020 19:33
Найти производную функции.

(3^x * tgx)' = (3^x)'*tgx + 3^x*(tgx)' =\\= 3^x*ln3*tgx + 3^x * \dfrac{1}{cos^2x} = 3^x(ln3*tgx + sec^2x).

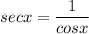Функция secx = \dfrac{1}{cosx} называется секанс.

Использованные табличные производные.

Тангенс: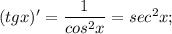 (tgx)' = \dfrac{1}{cos^2x} = sec^2x;

Показательная функция: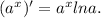 (a^x)' = a^xlna.

Использованная формула.

Производная произведения: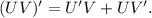 (UV)' = U'V + UV'.

ответ: 3^x(ln3*tgx + sec^2x).
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
anciferovalex anciferovalex  24.10.2020 12:17
что там написано я не понимаю...
dickosh97 dickosh97  24.10.2020 12:27
нужно узнать, что буквой а​...
СССС69 СССС69  24.10.2020 12:28
1. Сегодня Клыкхаузер побывал в гостях в деревне, и на обратную дорогу ему дали очень много пончиков. Он сел на поезд и поехал в город. Перед тем, как поезд сделалпервую остановку,...
ttm105 ttm105  24.10.2020 12:28
5 маляров покрасят забор за 9 дней. За сколько дней его покрасят 15 маляров? 1 маляр? 4 маляра? З маляра?​...
Плаоцтвтч Плаоцтвтч  24.10.2020 12:28
Сегодня мини тесты или простые задания...
AMORVL AMORVL  24.10.2020 12:28
Для награждения победителей математической олим­пиады школа купила 30 книг по 200 р. и по 250 р. — всего на 6650 р. Сколько было куплено тех и других книг? (Задача на уравнивание)...
toshakotik toshakotik  24.10.2020 12:29
Логические функции трех переменных....
Енотик83 Енотик83  24.10.2020 12:29
1. Три отрезка A1,A2, B1,B2 и C1,C2, не лежащие на одной плоскости имеют общую середину. Доказать, что плоскости A1,B1,C1и A2,B2,C2 параллельны.2. Дано: EMC=MCA и PEB=EBC.Доказать,...
Ronni05 Ronni05  19.05.2019 17:00
Придумать на составление уровнение...
Anonimka89 Anonimka89  19.05.2019 15:30
Найти промежутки выпуклости и точки перегиба : f(x) = x^2 + x^3 - 2...

Популярные вопросы