Найти производные или дифференциалы указанных порядков.
а) y= cosx+![\sqrt[3]{x}](/tpl/images/4164/8600/73e8b.png) +
+![\frac{1}{\sqrt[3]{x} }](/tpl/images/4164/8600/7407d.png) , dy=?
, dy=?
б) y=tg(7x+5)*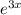 , y'(0)=?
, y'(0)=?
Другие вопросы по теме Математика
Популярные вопросы
- Разлелить на части сказку голая лягушка...
2 - Охарактерезуйте персонажів із повісті русалонька із 7-в...
1 - Какие природные особенности района развитию курортного хозяйства? (европейский...
3 - Переведите в прямую речь 1)my sister has broken my pencil 2)i take my little sister...
1 - 20 ! гидростат глубнной бомбы установлен на давление 2 мпа. на какой глубине в...
2 - Іть скласти 5 речень з риторичним звертанням....
1 - Укошику є тільки червоні і зелені кульки серед п яти навмання вибраних кульок є...
1 - Решите 1) оля увеличена некоторое число на 7%, а затем полученное число увеличила...
2 - Вездеход проехал половину пути с постоянной скоростью, модуль которой v1=10м/с....
2 - Водном треугольнике величины углов в градусах выраженны тремя различными числами....
1
Пошаговое объяснение:
а)
б)