найти прлизводную dy/dx функции
кажется, она неявная
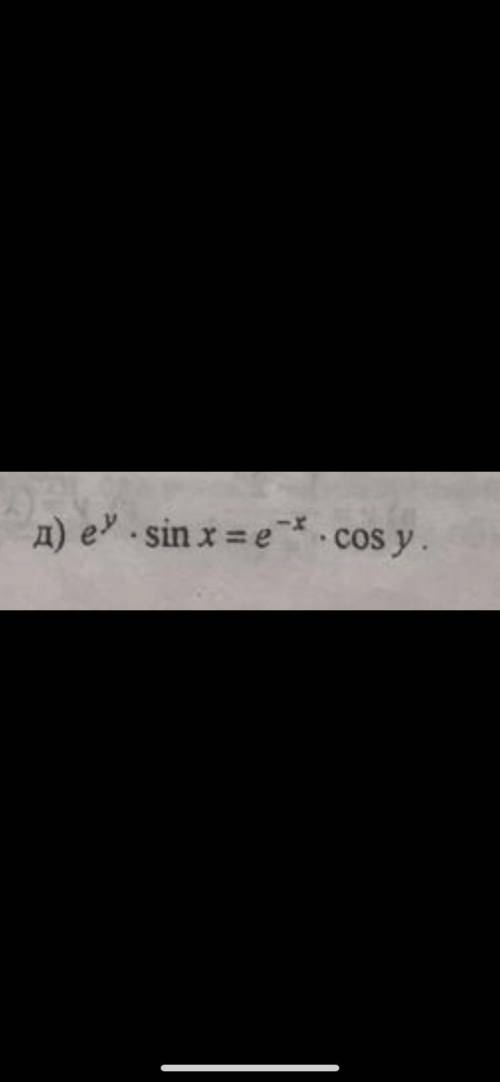
Другие вопросы по теме Математика
Популярные вопросы
- Расставь ударение н крыльце сидит пушистый кот . теплые лучи солнца согрели...
1 - Найдите наибольший делитель чисел 1)12 и 32 2)14 и 42 3)68 и 102 4)360...
3 - Ввазе стояло 11 роз.несколько роз завяло.в вазе осталось 7 роз.сколько...
3 - Колба заполнена сухим йодоводородом при нормальных условиях. затем колбу...
1 - Определение слов: сословия, феодальная раздробленность, франция, германия,италия,...
2 - Match the pictures to the words.then put them in alphabetical order.eraser,glue,chair,paperclips,blackboard,pincil...
1 - Сумрачно и величаво дымятся облаками скалистые и снежные горы. где однородные...
2 - \/l - lx = lll (переставить одну палочку хоть откуда и куда)...
1 - Сравните учения м.лютера и ж.кальвина. найдите черты сходства и различия.определите,в...
1 - Спишите . исправляя пунктуационные ошибки . подчеркните однородные члены...
1
Пошаговое объяснение:
Продифференцируем по x равенство
Тогда
ответ: y' = - ( e⁻ˣ cosy + e^y cosx )/ ( e^y *sinx + e⁻ˣ siny) .
Пошаговое объяснение:
e^y sinx = e⁻ˣ cosy ; y' - ?
( e^y)' sinx + e^y (sinx)' = ( e⁻ˣ)' cosy + e⁻ˣ (cosy)' ;
e^y * y' sinx + e^y cosx = - e⁻ˣ cosy - e⁻ˣ( siny)* y' ;
e^y * y' *sinx + e⁻ˣ( siny)* y' = - e⁻ˣ cosy - e^y cosx ;
y' ( e^y *sinx + e⁻ˣ siny) = - ( e⁻ˣ cosy + e^y cosx ) ;
y' = - ( e⁻ˣ cosy + e^y cosx )/ ( e^y *sinx + e⁻ˣ siny) .