1. Математика
  2. Найти пределы функций, не пользуясь

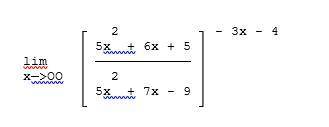
Найти пределы функций, не пользуясь правилом Лопиталя.


Найти пределы функций, не пользуясь правилом Лопиталя.

aaaaanastya92 aaaaanastya92    1   08.01.2022 00:11    0

Ответы
dobryninatonya dobryninatonya  08.01.2022 01:00

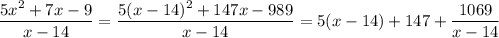
\lim\limits_{x\to \infty}\left[\dfrac{5x^2+6x+5}{5x^2+7x-9}\right]^{-3x-4} = \lim\limits_{x\to \infty}\left[1-\dfrac{x-14}{5x^2+7x-9}\right]^{-3x-4}. Далее \dfrac{5x^2+7x-9}{x-14} = \dfrac{5(x-14)^2+147x-989}{x-14} = 5(x-14)+ 147+\dfrac{1069}{x-14}\left[1-\dfrac{x-14}{5x^2+7x-9}\right]^{-3x-4} = \left[1-\dfrac{x-14}{5x^2+7x-9}\right]^{\frac{5x^2+7x-9}{x-14}-8x-81-\frac{1069}{x-14}}. Теперь можем разбить на произведение нескольких частей: \left[1-\dfrac{x-14}{5x^2+7x-9}\right]^{\frac{5x^2+7x-9}{x-14}}\left[1-\dfrac{x-14}{5x^2+7x-9}\right]^{-8x-81}\left[1-\dfrac{x-14}{5x^2+7x-9}\right]^{-\frac{1069}{x-14}}}. 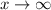Предел при x\to \infty первого множителя равен 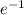e^{-1}, а последнего множителя -- 1. 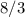Второй множитель очень напоминает исходный, он отличается в 8/3 раза (на постоянную 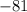-81 можно забить, она потом перейдет в единицу точно так же, как и последний множитель). 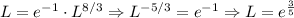Искомый предел равен L = e^{-1}\cdot L^{8/3} \Rightarrow L^{-5/3} = e^{-1} \Rightarrow L = e^{\frac{3}{5}}.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Radmirka1337 Radmirka1337  17.05.2019 18:44
Выполни действия, применяя законы сложения 58,8 + (215 + 1,2)...
Куликова2006 Куликова2006  17.05.2019 18:44
Размеры ёмкость в форме кубойда составляют 32см , 3 дм и 0,4м . можно ли налить в эту ёмкость 40 л воды ? преобразуйте в стандартные единицы а)35 мл = в)2,4га= б)0,25т...
edynorozhok edynorozhok  17.05.2019 18:46
Впервый ночь день рабочие отремонтировали 40 метров дороги, во второй день - 25 метров. им осталось еще отремонтировать на 8 метров больше, чем они уже отремонтировали....
tel9057969295p0bj7i tel9057969295p0bj7i  17.05.2019 18:46
Найдите значение выражения выбирая удобный порядок вычисления 6, 13 + 1, 98 + ( - 4,27) + ( - 5,13) + 3,27...
tyyyyyj tyyyyyj  17.05.2019 18:46
1.найдите объем прямоугольного параллелепипеда с измерениями 2,5см, 4см и 5см 2. переведите дробь 6/8 из обыкновенной в десятичную 3. в течение месяца саша играл...
1903vita 1903vita  17.05.2019 18:47
4. вычисли.(1000 - 794) 3=(645 - 65): 5=(909 - 694) 2=167.3 +97=(345 + 564): 3=(887 - 694) - 4=(12 + 458): 2=630 - 625: 5=заранее ​...
ivanapushkin10 ivanapushkin10  17.05.2019 18:47
Найдите сумму цифр 150 члена чисел 2 3 5 6 7 8 10 11 который не является целым квадратом​...
nina19862 nina19862  17.05.2019 20:00
Коля и петя вскапывают грядку за 10 мин, а один коля – за 15 мин. за сколько минут вскапывает грядку один петя?...
руслан794 руслан794  17.05.2019 20:00
Как профессия косметолог влияет на окружающую среду? (отрицательно, как именно? )...
roman2223q roman2223q  17.05.2019 18:48
Расположите в порядке возрастания следующие числа: 6/13 ,1, 2/13 ,10/5...

Популярные вопросы