1. Математика
  2. Найти предел[tex]\lim_{x\to\infty}x^{\alpha}b(x,\alpha)

Найти предел
\lim_{x\to\infty}x^{\alpha}b(x,\alpha)
если
\alpha > 0

engelsvova engelsvova    3   21.08.2019 00:53    0

Ответы
Matveykaka Matveykaka  05.10.2020 08:20

\Gamma(\alpha)

Пошаговое объяснение:

Определение бета-функции:

\displaystyle B(a,b)=\int_0^1t^{a-1}(1-t)^{b-1}\,dt

Подставляем:

\displaystyle\lim_{x\to\infty}\int_0^1x^\alpha t^{x-1}(1-t)^{\alpha-1}\,dt=\dots

Делаем замену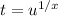 t=u^{1/x}:

\displaystyle\dots=\lim_{x\to\infty}\int_0^1x^\alpha u^{1-1/x}(1-u^{1/x})^{\alpha-1}\frac{u^{1/x}\,du}{ux}=\\=\lim_{x\to\infty}\int_0^1\left[x(1-u^{1/x})\right]^{\alpha-1}\,du=\int_0^1\left[\lim_{x\to\infty}\frac{1-u^{1/x}}{1/x}\right]^{a-1}du=\dots

Посмотрим на предел поближе:

\displaystyle\lim_{x\to\infty}\frac{1-u^{1/x}}{1/x}\right=\lim_{y\to+0}\frac{1-e^{y\ln u}}{y}=-\ln u

Вносить предел под знак интегрирования было можно: легко проверить, что при убывании y функция под знаком предела монотонно стремится к предельной функции, которая непрерывна на (0, 1).

Осталось сделать замену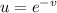 u=e^{-v} и получится определение гамма-функции:

\displaystyle\dots=\int_0^1\left[-\ln u\right]^{a-1}du=\int_0^\infty v^{a-1}e^{-v}\,dv

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
bogdansoroka20 bogdansoroka20  28.07.2019 13:10
Для нового помещения фирма закупила 14 новых столов,а стульев в 4 раза больше.все купленные стулья поставили в 7 комнат ,поровну в каждую.сколько новых стульев в каждой комнате?...
goldshell goldshell  28.07.2019 13:10
Чему равно наивероятнейшее число нестандартных среди 500 деталей, если вероятность быть нестандартной для каждой из них равно 0,035?...
Motia2k17 Motia2k17  28.07.2019 13:10
Написать эссе мое представление о современном детстве...
пупс110 пупс110  28.07.2019 13:10
Чему равно радиус окружности описанной около квадрата со стороной 8 см?...
куколку куколку  28.07.2019 13:10
Население города архангельска в 2013 году составляло 350 985 человек. на сколько процентов уменьшилось население архангельска в 2014 году, если по данным государственной статистики...
vika45584 vika45584  28.07.2019 13:10
Нарисуй один из памятников и сделай краткое описание, используй предложенный тебе план. 1.название памятников и его предназначение. 2.время и место сооружения. 3.судьба памятника...
LeНин LeНин  28.07.2019 13:10
Докажите что треугольник равнобедренный если его стороны являются медианами квадрата...
krisrinanovokr krisrinanovokr  28.07.2019 13:10
Вметро 20% пассажиров читают газеты. из них 65%-мужчины. сколько процентов пассажиров метро составляют мужчины, читающие газеты? , решить((...
Маря04 Маря04  28.07.2019 13:10
Машина проехала 84 км, что составляет шесть тринадцатых всего пути. найди, чему равен весь путь. мяук : 3...
azs194karelin azs194karelin  28.07.2019 13:20
Найдите корень уравнения: (x-0,9)^5=-1...

Популярные вопросы