Найти предел !
С решением и ответом !)
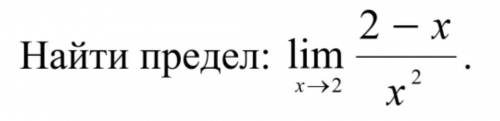
Другие вопросы по теме Математика
Популярные вопросы
- О гоадусов по ференгету и цельсию...
1 - . Собственная скорость катера равна 15 км/ч, скорость течения5реки—...
1 - «Балапан», «Арна» сөздерін септеңіздер. (Склоните слова в скобках)...
3 - 5. Отгадай загадку. Какая часть речи найти ответ? На первую ступеньку...
1 - Two perpendicular forces act on a 400 g object. The object moves...
1 - 1-тапсырма: Дулат Исабековтың «Әпке» шығармасы бойынша сұрақтарға...
3 - компоненты топлива в двигатель ракеты подаются сос скоростью 200м/с,...
3 - Соотнесите средства художественной выразительности с примерами из...
1 - сумма первых 5 членов арифметикой прогрессии равна 5 найдите разность...
1 - I. Писатель (вопросы о жизни и творчестве писателей, представленных...
2
В данном случае имеется предел функции, состоящей из двух слагаемых - числителя и знаменателя.
1. Сначала рассмотрим числитель:
a) Сокращаем общий множитель. Для удобства представим числитель в виде произведения двух множителей:
(x + 4)(x - 5)
b) Применим свойство арифметики к разности квадратов:
(x + 4)(x - 5) = x^2 - 5x + 4x - 20 = x^2 - x - 20
2. Затем рассмотрим знаменатель:
a) Выделим общий множитель:
x^2 - 9 = (x - 3)(x + 3)
3. Теперь можем записать исходное выражение в виде отношения двух функций:
f(x) = (x^2 - x - 20) / (x^2 - 9)
4. Для нахождения предела данного выражения используем правило Лопиталя, так как в числителе и знаменателе присутствуют полиномы с одинаковой степенью:
a) Находим производные числителя и знаменателя:
f'(x) = (2x - 1) / (2x)
g'(x) = (2x)
b) Заменяем исходное выражение на предел отношения производных:
lim(x->∞) (x^2 - x - 20) / (x^2 - 9) = lim(x->∞) (f'(x) / g'(x))
5. Вычисляем предел отношения производных:
a) Подставляем бесконечность в производные:
lim(x->∞) (2x - 1) / (2x) = lim(x->∞) 2 - 1/x = 2 - 0 = 2
6. Таким образом, предел данной функции равен 2.
Ответ: lim(x->∞) (x^2 - x - 20) / (x^2 - 9) = 2.
Обоснование:
Мы применили правило Лопиталя, которое позволяет найти предел отношения двух функций, если они оба стремятся к бесконечности или к 0. В нашем случае, оба числитель и знаменатель стремятся к бесконечности при x, стремящемся к бесконечности, и мы получаем конечное число 2.