Найти предел. Правилом Лапиталя пользоваться нельзя. Желательно решить через эквивалентность.з
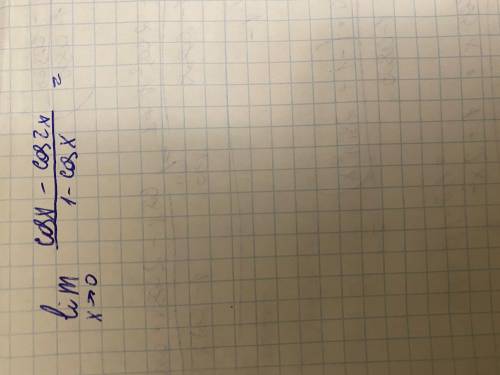
Другие вопросы по теме Математика
Популярные вопросы
- Запишите предложения, употребляя вместо точек союзное слово который в нужной...
1 - Число 240 разделили части прямопропорциональные 2 : 3 : 5. Найдите суммусамой...
1 - При давлении 5∙106 Па газ занимает объем 2∙10-2м3. Под каким давлением будет...
3 - Себестоимость 1 т подсолнечника который выращивается на 1-м участке составляет...
3 - Тело вращается вокруг оси OX по закону φ=7t2−2t+3φ=7t2−2t+3. В момент времени...
3 - Найти площадь боковой поверхности прямой призмы, у которой в основаниях лежат...
3 - 7) Социальная группа с наследственными правами и обязанностями (дворянство,...
1 - Стислий план. Джури характерники ...
2 - Решите уравнение с подробным объяснением...
3 - Which sentences can be changed into the Passive Voice? 1. We have tied two...
1
3
Пошаговое объяснение:
Разложим в ряд тейлора cosx и cos2x до o(x^2)
получаем cosx = 1 - (x^2)/2 + o(x^2)
cos2x = 1 - ((2x)^2)/2 + o(x^2) = 1 - 2x^2 + o(x^2) (тут уже не совсем разложение в ряд тейлора, но так делать можно и нужно)
подставляем в предел:
lim(1-(x^2)/2 - (1 - 2x^2) + o(x^2))/(1 - (1 - (x^2)/2) + o(x^2)) = lim(3/2 * x^2 + o(x^2))/(1/2 * x^2 + o(x^2)) дальше делим всё на x^2 и получаем lim(3/2 + o(x^2))/(1/2 + o(x^2)) = 3/2 / 1/2 = 3