1. Математика
  2. Найти полный дифференциал

Найти полный дифференциал функции z=sqrt(y) * arcsin x^2 z=sin x^2 + cos^2 (x)

Kachalova54 Kachalova54    3   01.06.2019 10:00    0

Ответы
khorolovgusenoy2lzx khorolovgusenoy2lzx  02.07.2020 16:19

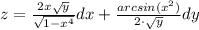
ответ: z=\frac{2x\sqrt{y} }{\sqrt{1-x^4} }dx +\frac{arcsin(x^2)}{2\cdot\sqrt{y}}dy

dz = (2x·cos(x²) - sin(2x))dx

Пошаговое объяснение:

Найти полный дифференциал функции  

z = √(y)·arcsin(x²)

Формула полного дифференциала функции:

dz=\frac{\partial z}{\partial x}dx +\frac{\partial z}{\partial y}dy

Найдем частные производные

\frac{\partial z}{\partial x}=(\sqrt{y}\cdot arcsin(x^2))' =\sqrt{y}\cdot(arcsin(x^2))'=\sqrt{y}\cdot\frac{1}{\sqrt{1-x^4} }\cdot (x^2)'=\frac{2x\sqrt{y} }{\sqrt{1-x^4} }

\frac{\partial z}{\partial y}=(\sqrt{y}\cdot arcsin(x^2))' =(\sqrt{y})'\cdot arcsin(x^2)=\frac{1}{2\cdot\sqrt{y}}\cdot arcsin(x^2)=\frac{arcsin(x^2)}{2\cdot\sqrt{y}}

z=\frac{2x\sqrt{y} }{\sqrt{1-x^4} }dx +\frac{arcsin(x^2)}{2\cdot\sqrt{y}}dy

Найти полный дифференциал функции  

z = sin(x²) + cos²(x)

Так как функция  z зависит только от одной переменной то формула полного дифференциала

dz=\frac{\partial z}{\partial x}dx

Находим производную

z' = (sin(x²) + cos²(x))' = cos(x²)·(x²)' + 2cos(x)·(cos(x))' = 2x·cos(x²) - 2sin(x)·cos(x) = 2x·cos(x²) - sin(2x)

dz = (2x·cos(x²) - sin(2x))dx

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Naniko1515 Naniko1515  06.05.2020 11:46
Длина забора, окружающего участок квадратной формы, равна 76 м. Чему равна площадь этого участка?¹​...
Зайка20005 Зайка20005  06.05.2020 11:46
ЭТО ЗАДАЧА, нужно все решать Студент знає 26 питань із 30 програми. Знайти ймовірність, що студент із трьох запитань відповів: • а) на одне запитання; • б) на всі запитання;...
HrenSGori HrenSGori  06.05.2020 11:46
В полярной системе координат построить кривую, заданную уравнением в декартовых координатах...
Alexkusaiko Alexkusaiko  06.05.2020 11:46
Найти Точки максимума, минимума функции y=2x^3-12x^2+18x...
провривррф провривррф  06.05.2020 11:46
Два туристи вийшли одночасно з двох міст відстань між якими 38км,і зустрілися через 2год.З якою швидкістю йшов кожний якщо перший до зустрічі пройшов на 2км більше,ніж...
SuperArtem52 SuperArtem52  06.05.2020 11:46
Ширина прямокутника 20см, а довжина 125% від його ширини. Знайти периметр прямокутника...
вика134475 вика134475  06.05.2020 11:46
Решите прикреплён) №2 Даны координаты точки. Определи, на которой координатной оси находится данная точка. Точка K(−28;0) находится на оси №3 Даны координаты точки....
dashaR06032006 dashaR06032006  06.05.2020 11:45
Площiна на якiй задано сестему координат називають?​...
1Kotejka1 1Kotejka1  06.05.2020 11:46
Магазин концтоваров закупает набор из 15 фломастеров по оптовой цене 250 рублей за один набор и продает с наценкой 20%. сколько рублей будут стоит 3 таких набора,купленных...
ялюблюкотиков ялюблюкотиков  06.05.2020 11:44
Масса тигра равна 272 кг,льва - 227 кг.Масса белой медведицы на 501 кг больше,чем масса тигра и льва,вместе взятых.Найдите массу белой медведицы.Выразите массы животных...

Популярные вопросы