Найти площадь фигуры ограниченной линиями
y=-x^2+9 и y=0 (предварительно сделав рисунок).
Другие вопросы по теме Математика
Популярные вопросы
- Чем отличается тропосфера от стратосферы по плотности и массе воздуха по изменению...
1 - Вчём величие писателя солженицына, по мнению французского критика жоржа нива? дайте...
2 - Вравнобедренном треугольнике abc с основанием ac проведена высота am. найдите угол...
1 - Сочинение рассуждение на тему зачем нужны частицы?...
1 - Надо рассазатьпро москву. сколько в ней храмов . и побольше...
2 - Когда в москве 5 часов вечер в барнауле 900 сколько времени в москве когда в барнауле...
1 - На изготовление одного кольца идёт 4 см 6 мм проволоки .когда из куска проволоки...
2 - Спиши раскрывая скобки укажи наклонение глаголов объясни значение пословиц. сказал...
1 - Докажите что четырехугольник с вершинами а(3.5.4) в(5 0 2) ромб. в(5 0 2) с 1 1...
2 - 1)запиши все равенства, которые соответствуют схемам ⬜*⬜=⬜ ⬜: ⬜=⬜ 2)а какие равенства...
2
36
Пошаговое объяснение:
Первый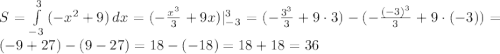 Второй
Второй
Так как график квадратичной функции симметричен относительно оси Oy, то площадь всей фигуры можно найти как удвоенную площадь одной из половин, например правой: