1. Математика
  2. Найти площадь фигуры ограниченной

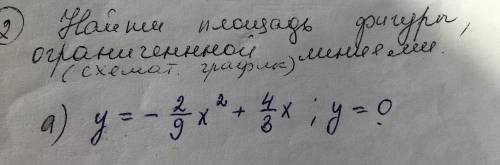
Найти площадь фигуры ограниченной линиями
(Схема, график)


Найти площадь фигуры ограниченной линиями (Схема, график)

tanya665444 tanya665444    1   27.02.2021 09:57    0

Ответы
airamoon airamoon  29.03.2021 10:01

Відповідь:

S = 8 см²

Покрокове пояснення:

По формуле Ньютона-Лейбница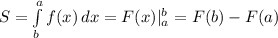 S=\int\limits^a_b {f(x)} \, dx =F(x)|^b_a=F(b)-F(a) найдем площадь фигуры.

Рисуем график функции и обозначаем площадь какой фигуры мы будем искать (примерный график на фото ниже). a и b - пределы, на которых лежит фигура ограниченная линиями y (их можно увидеть на рисунке). Теперь подставляем значение в нашу формулу:

S=\int\limits^6_0 ({-\frac{2}{9}x^2+\frac{4}{3}x}) \, dx =(-\frac{2x^3}{27}+\frac{2x^2}{3})|^6_0=(\frac{-2*6^3}{27}+\frac{2*6^2}{3})-0=-\frac{2*216}{27}+24=-2*8+24=-16+24=8

Итого, площадь фигуры ограниченной линиями равна 8 см².


Найти площадь фигуры ограниченной линиями (Схема, график)
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Zaharza1 Zaharza1  08.09.2019 20:20
На меховую фабрику 63 овечьи шкуры. в первый день сшили 7 полушубков, затратив по 7 шкур на каждый из них. сколько шкур осталось на фабрике?...
Mariska4 Mariska4  08.09.2019 19:17
145. начертите окружность (r = 5 см) с центром в точке 0.постройте следующие фигуры: 1) точку а, принадлежащую окружности; точку в, принад-лежащую кругу; точку с, не принадлежащую...
galina157 galina157  08.09.2019 19:17
Можете решить то что обведено просто времени нету самой решать и некоторые я не понимаю...
Ks113 Ks113  08.09.2019 19:17
7697357 округлить до сотен тысяч...
2003tanya 2003tanya  08.09.2019 19:16
Найдите производную у=4х^2-10x+ 25/х​...
kitten0908 kitten0908  08.09.2019 20:20
8в третьей степени : 4 четвертой степени...
anonymus98 anonymus98  08.09.2019 20:20
Найдите значение выражения (√48-√3)*√3...
  08.09.2019 20:20
На рисунке два треугольника разлеляют листок бумаги на 6 частей(шестая часть-это то,что останется на листе,если вырезать оба треугольника).нарисуйте два четырёхугольника,которые...
lu000001 lu000001  08.09.2019 20:20
Решите уравнение : а ) 127 + y =357 - 85 б)125 +y-85=65...
суперкотик4 суперкотик4  08.09.2019 20:20
Строчки о природе из любых известный стихотворений...

Популярные вопросы