Найти оригинал f(t) за заданным изображением F(p)
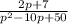
Другие вопросы по теме Математика
Популярные вопросы
- 7. Запишите кратко условие задачи и решите её.Пружину, к которой подвешен...
2 - Угол АОС развёрнутый, а ОС – луч. Найдите градусные меры углов АОС и...
3 - на казахском языке слово Таяғын...
2 - мне с этим С уравнения найдите числа, если первое число больше второго...
2 - Task 2 Read the text and complete it with the phrases (a-e). There is...
2 - Основой прямой призмы является равносторонний треугольник с длиной стороны...
3 - Б.Н.Полевой Повесть о настоящем человеке 1) Как фамилия главного героя?А)...
3 - Одиничний дієприслівник треба відокремлювати комами в реченні (розділові...
2 - На координатной плоскости нарисуй точку C(−4;−9), точку F(−2;−7) и точку...
3 - Х саны 40 тан артык және 65 тен кем...
1
Пошаговое объяснение:
В силу линейности, имеем
Используя таблицу оригиналов и изображений, получим