1. Математика
  2. Найти общее решение (общий интеграл)

Найти общее решение (общий интеграл) дифференциального уравнения первого порядка, надо подробное решение))


Найти общее решение (общий интеграл) дифференциального уравнения первого порядка, надо подробное реш

АлександрЧерепов АлександрЧерепов    1   13.02.2022 21:35    0

Ответы
Высплюсенье Высплюсенье  13.02.2022 22:00

(Метод Лагранжа).

y'+y=\cos{x};y'+y=0; \frac{dy}{dx} =-y; \frac{dy}{y}=-dx; \int{\frac{dy}{y} }=-\int{dx}; \ln|y|=-x+C;ln|y|=\ln{e^{-x}}+\ln{C}; \ln{y}=\ln{Ce^{-x}}; y=Ce^{-x}

Произвольную постоянную примем за функцию от x.

y=C(x)e^{-x}; y'=C'(x)e^{-x}-C(x)e^{-x}.

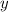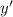Подставим y и y' в исходное уравнение:

C'(x)e^{-x}-C(x)e^{-x}+C(x)e^{-x}=\cos{x}; C'(x)e^{-x}=\cos{x}; \frac{d(C(x))}{dx}=\frac{\cos{x}}{e^{-x}}d(C(x))=\frac{\cos{x}dx}{e^{-x}}; \int{d(C(x))=\int{\frac{\cos{x}dx}{e^{-x}}}; C(x)=\int{\frac{\cos{x}dx}{e^{-x}}};

Отдельно найдем полученный неопределенный интеграл:

\int\frac{\cos{x}dx}{e^{-x}}=\int{e^x\cos{x}}dx;int{e^x\cos{x}}dx=\left[u=e^x; du=e^xdx\atop dv=\cos{x}dx;v=\sin{x}\right]=e^x\sin{x}-\int{e^x\sin{x}dx.}int{e^x\sin{x}dx=\left[u=e^x; du=e^xdx\atop dv=\sin{x}dx;v=-\cos{x}\right]=-e^x\cos{x}+\int{e^x\cos{x}}dx.

Отсюда получаем что:

\int{e^x\cos{x}}dx=e^x\sin{x}-(-e^x\cos{x}+\int{e^x\cos{x}dx});2\int{e^x\cos{x}}dx=e^x\sin{x}+e^x\cos{x}int{e^x\cos{x}}dx=\frac{e^x}{2}(\sin{x}+\cos{x})+C_2

Отсюда получаем что:

C(x)=\frac{e^x}{2}(\sin{x}+\cos{x})+C_2

Теперь подставим в формулу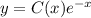 y=C(x)e^{-x}:

y=\frac{1}{e^x}\Big(\frac{e^x}{2}(\sin{x}+\cos{x})+C_2 \Big) =\frac{1}{2}(\sin{x}+\cos{x}) +e^{-x}C_2

В итоге окончательно получаем:

\boxed{y=\frac{1}{2}(\sin{x}+\cos{x})+Ce^{-x}}

(Метод Бернулли)

y'+y=\cos{x}

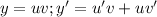Пусть y=uv; y'=u'v+uv' тогда:

u'v+uv'+uv=\cos{x}; u'v+u(v'+v)=\cos{x} потребуем, чтобы v'+v=0 тогда:

\frac{dv}{dx}+u=0;\frac{dv}{v}=-dx; \int{\frac{dv}{v} }=-\int{dx};\ln{v}=-x \Rightarrow v=e^{-x}

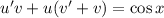Подставим найденное значение v в u'v+u(v'+v)=\cos{x}:

u'e^{-x}+u(e^{-x}-e^{-x})=\cos{x};u'=\frac{\cos{x}}{e^-x} \Rightarrow u=\int{e^x\cos{x}}dx

В предыдущем данный интеграл был найден методом интегрирования по частям, поэтому не будет здесь его искать а просто подставим уже найденный.

u=\frac{e^x}{2}(\sin{x}+\cos{x})+C но y=uv тогда:

y=e^{-x}(\frac{e^x}{2}(\sin{x}+\cos{x})+C )=\frac{1}{2}(\sin{x}+\cos{x})+Ce^{-x} Отсюда получаем:

\boxed{y=\frac{1}{2}(\sin{x}+\cos{x})+Ce^{-x} }

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Бекзат2000 Бекзат2000  20.01.2021 11:23
Написать небольшое сочинение-эссе Почему вежливые слова называют волшебными? 7-8 предложений​ это русский...
qwertyqwerty1233 qwertyqwerty1233  20.01.2021 11:23
Тура санды теңдіктің қасиетін пайдаланып: 1) 3,6 - (- 4) = 72 :(- 5) теңдігінің екі жақ бөлігіне де – 5,6 санын;24 санын қосыңдар.52) 2,4 12,9 = 63 : (- 6)63 : (- 6) теңдігінің...
kakaha7 kakaha7  20.01.2021 11:23
В урожайный год фермеру удалось собрать 18 ц/га, а в не урожайный только 8ц/га. Какой урожай пшеницы он собирал в каждый из этих годов, если под пшеницу у него отведено 300...
vabimGogolev vabimGogolev  20.01.2021 11:24
2. Бірінші шүмек хауызды 6 сағатта толтырады. Ал хауызды екінші шүмекпен  толтырса, оған бірінші шүмекке кеткен уақыттың үштен екі -сіндей уақыт қажет.  Егер екі шүмекті...
Limon2601 Limon2601  20.01.2021 11:24
если напишите какую то бурду что бы получить , кину жб)​...
володия володия  20.01.2021 11:24
вот правильный ответ не догонить в 18 проверино сори ячто я пишу с ошибками ответ не логонить в 18 раз...
мамадочп4а мамадочп4а  20.01.2021 11:24
Визнач площу зафарбованої на малюнку фігури, якщо діаметр круга дорівнює 3,2 см, а довжина сторони квадрата - 1,1 см. (5 Вправа)...
vshapovalova21 vshapovalova21  20.01.2021 11:25
На даній прямій розташовані точки M(1;1) і P(2;3). Напиши рівняння цієї прямої. (подбай, щоб коефіцієнти були цілими)...
dolloc dolloc  20.01.2021 11:25
Линейное уравнение с одной переменной, содержащее переменную под знаком модуля. Урок 1 Верных ответов: 24–43–22Нашли ошибку на сайте?ZERO.kz​...
юрпа юрпа  20.01.2021 11:25
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить две различных фотографии. Сколькими это можно сделать, если ни одна страница газеты не должна...

Популярные вопросы