Найти общее решение (общий интеграл) дифференциального уравнения
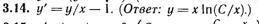
Другие вопросы по теме Математика
Популярные вопросы
- 1) The Van Gogh Museum will ___ 135 of his paintings. 2) The curriculum ___ courses...
3 - Listening & Writing 5.L6 Listen and complete the fact file. . 6 a) Fact file...
1 - Порівняйте почуття розлуки у віршах Р. Бернса і К. Симонова...
2 - 14.12. Постройте график функции f(x) = -2х2 - х + 7 и, используя график, найдите:...
1 - 1. Перечислите некоторые из прав потребителей. Какие права имеют производители...
3 - Указать вид связи( согласование , управление, примыкание) Боится встречи,новый...
1 - Запишите все целые числа которые больше -5 и меньше 5...
2 - Как изменяется магнитный поток пронизывающий витки катушки...
2 - I (to live) in a small town and there are no big galleries and museums in it. But...
1 - Задание 2. Соотнесите верно идеи социалистов: 1 Фердинанд Лассаль 2 Карл Маркс...
3
ЛДУ
Замена:
общее решение
Відповідь:
Покрокове пояснення:
у'=у/х -1
Введем замену u=y/x → y'=u+xu'
u+xu'=u-1
u'= -1/x
du= -1/x dx
∫du= -∫1/x dx
u= - ln|x|+C вспомним о замене
y/x = ln(1/|x|)+C
y= x( ln|1/x|+C)
Если за константу взять lnС, то будем иметь
у=х (lnС/|х|)