Найти общее решение дифференциальных уравнений:
1) y-xy'=x*sec(y/x)
2) xy'=y-x*e^(y/x)
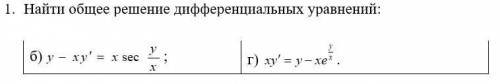
Другие вопросы по теме Математика
Популярные вопросы
- , На некотором сайте пароли пользователей должны содержать от трёх до пяти...
3 - А..К.Е.М___.В АЕ=ВЕ АК=ЕМ доказать КЕ=МВ...
1 - Как нужно ударить мяч чтобы он летел точно в 9???...
2 - Написати міні-твір на тему: Як слово о полку Ігоревім перегукується з нашим...
3 - Что делать,если новенький в классе думает,что он лучше всех и как развести...
3 - Электрическая лампа рассчитана на напряжение 220 В и силу тока 0,45 А. Вычислите...
3 - Велосипедист проехал 24 км что составило 30% пути, Сколько километров им...
3 - Составить сообщение на тему Троицкая церковь в Козьмодемьянске 5 класс...
2 - назвать успехи внешней политики России (победы, завоевания)выписать даты...
3 - Что такое Земля? Объясните мне ....
2
1) y - xy' = x * sec(y/x)
Для начала давайте заменим переменные. Пусть u = y/x, тогда y = ux. Заменим y и y' в исходном уравнении:
ux - x(du/dx) = x * sec(ux/x)
ux - x(du/dx) = x * sec(u)
Теперь преобразуем уравнение, чтобы оно стало более простым:
ux - x(du/dx) = x * (1/cos(u))
Разделим оба выражения на x, чтобы получить:
u - (du/dx) = 1/cos(u)
Давайте переместим все члены с u на одну сторону и все члены с x на другую:
u - 1/cos(u) = (du/dx)
Теперь давайте разделим уравнение на (u - 1/cos(u)):
(dx)/(du) = 1/(u - 1/cos(u))
Заметим, что это уравнение разделяющихся переменных. Разделим обе части уравнения:
dx = (1/(u - 1/cos(u))) * du
Теперь, давайте проинтегрируем обе части уравнения:
∫dx = ∫(1/(u - 1/cos(u))) * du
Интегрирование может быть довольно сложным для этого уравнения, однако мы можем сделать замену переменной z = u - 1/cos(u), чтобы упростить его:
∫dx = ∫(1/z) * du
Теперь, чтобы проинтегрировать это уравнение, нам нужно использовать метод интегрирования по частям:
∫dx = ∫(1/(z)) * du
x = ∫(1/(z)) * du
x = ln|z| + C
Теперь, вернемся к изначальной замене переменной:
z = u - 1/cos(u)
И подставим обратно значение z в уравнение:
x = ln|(u - 1/cos(u))| + C
Таким образом, общим решением этого уравнения является:
y = (xln|(y/x - 1/cos(y/x))|) + C
Теперь перейдем ко второму уравнению:
2) xy' = y - xe^(y/x)
Для начала, давайте заменим переменные и введем новую переменную z = y/x, тогда y = zx.
Заменим y и y' в исходном уравнении:
x(dz/dx) = zx - xe^(zx/x)
Разделим уравнение на x:
(dz/dx) = z - e^(z)
Для этого уравнения, у нас есть нелинейное дифференциальное уравнение первого порядка. К сожалению, нет простого аналитического общего решения для этого уравнения. Однако, мы можем найти приближенное решение, используя численные методы или разложение в ряд Тейлора.