Найти общее решение дифференциального уравнения xy'-2y=2x^4. нужно
Ответы
Решить 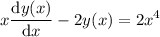 для
для 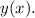
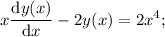
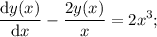
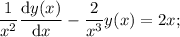
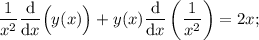
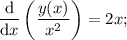
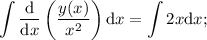
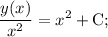
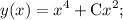
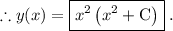
ПОКАЗАТЬ ОТВЕТЫ
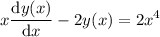 для
для 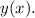
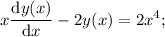
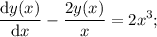
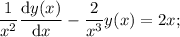
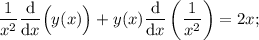
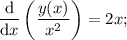
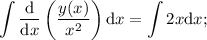
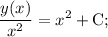
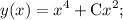
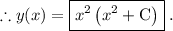
Другие вопросы по теме Математика
Популярные вопросы
- Выпишите из текста Б последнее предложение. Докажите, что в нёи одно обстоятельство....
2 - Почему Цезаря не предали забвению а наоборот возвысили?...
2 - 9.Звуковые волны похожи на A) на прямые линииБ) на кругиВ) на квадратики 2 класс...
1 - При нарушении микрофлоры толстого кишечника затрудняеться синтез витамина 1)А...
2 - доклад о экологическом состоянии Республики Казахстан не игнорте очень сор...
1 - Бишкек шаарына 143 жыл мини сочинение...
3 - площадь джизакской области 21100 км а площадь самаркандской области на 4300...
2 - A) Постройте треугольник KLM, по стороне KL=5см, угол K= 40 градусов, угол L=...
2 - Прочитай высказывание Почему люди отдыхают?...
1 - Инициативность быстро принимать решения. да нет 2. Умение быстро схватывать...
1